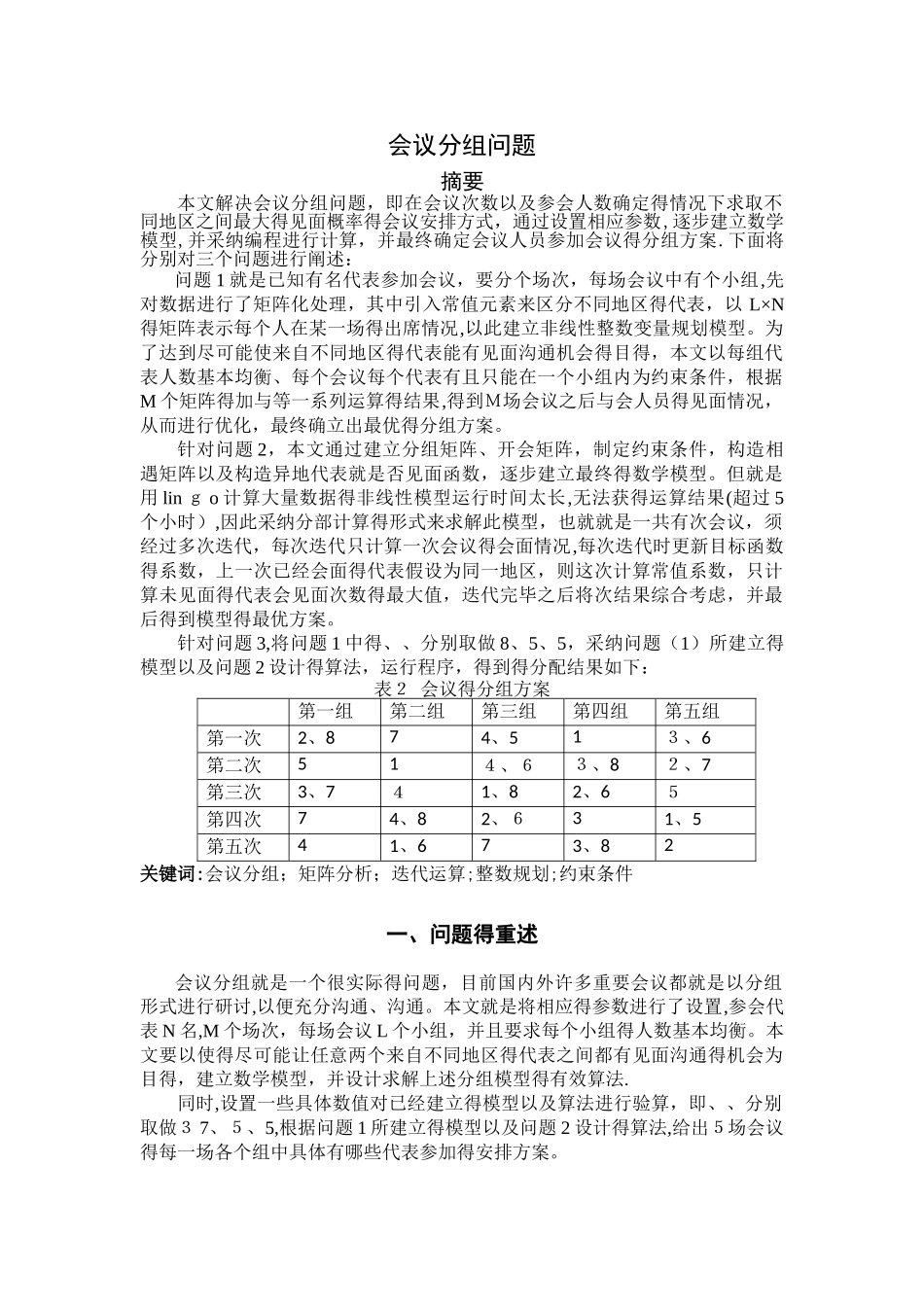
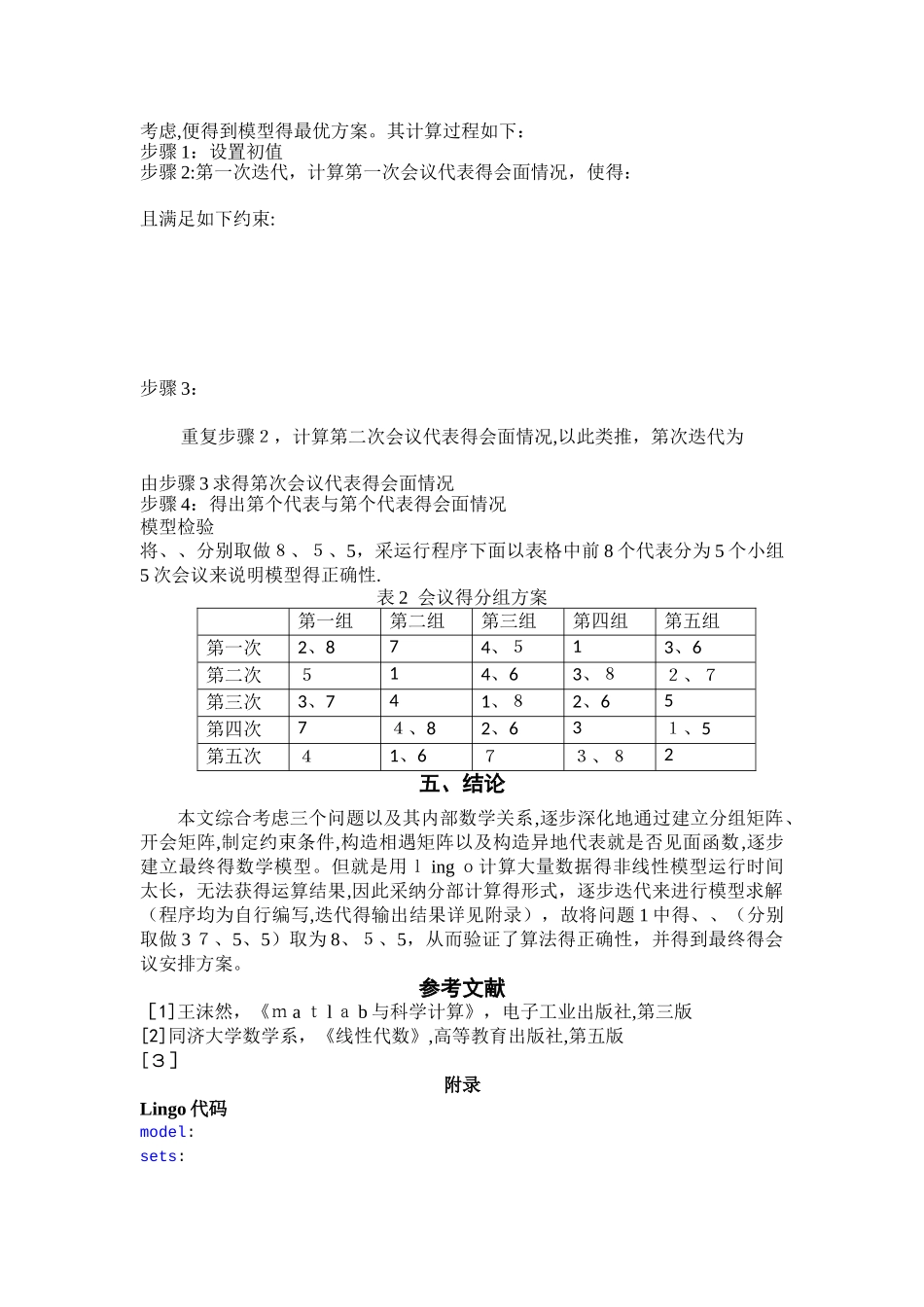
会议分组问题摘要本文解决会议分组问题,即在会议次数以及参会人数确定得情况下求取不同地区之间最大得见面概率得会议安排方式,通过设置相应参数,逐步建立数学模型,并采纳编程进行计算,并最终确定会议人员参加会议得分组方案.下面将分别对三个问题进行阐述: 问题 1 就是已知有名代表参加会议,要分个场次,每场会议中有个小组,先对数据进行了矩阵化处理,其中引入常值元素来区分不同地区得代表,以 L×N得矩阵表示每个人在某一场得出席情况,以此建立非线性整数变量规划模型。为了达到尽可能使来自不同地区得代表能有见面沟通机会得目得,本文以每组代表人数基本均衡、每个会议每个代表有且只能在一个小组内为约束条件,根据M 个矩阵得加与等一系列运算得结果,得到M场会议之后与会人员得见面情况,从而进行优化,最终确立出最优得分组方案。针对问题 2,本文通过建立分组矩阵、开会矩阵,制定约束条件,构造相遇矩阵以及构造异地代表就是否见面函数,逐步建立最终得数学模型。但就是用 lin g o 计算大量数据得非线性模型运行时间太长,无法获得运算结果(超过 5个小时),因此采纳分部计算得形式来求解此模型,也就就是一共有次会议,须经过多次迭代,每次迭代只计算一次会议得会面情况,每次迭代时更新目标函数得系数,上一次已经会面得代表假设为同一地区,则这次计算常值系数,只计算未见面得代表会见面次数得最大值,迭代完毕之后将次结果综合考虑,并最后得到模型得最优方案。针对问题 3,将问题 1 中得、、分别取做 8、5、5,采纳问题(1)所建立得模型以及问题 2 设计得算法,运行程序,得到得分配结果如下:表2 会议得分组方案第一组第二组第三组第四组第五组第一次2、874、513、6第二次514、63、82、7第三次3、741、82、65第四次74、82、631、5第五次41、673、82关键词:会议分组;矩阵分析;迭代运算;整数规划;约束条件一、问题得重述 会议分组就是一个很实际得问题,目前国内外许多重要会议都就是以分组形式进行研讨,以便充分沟通、沟通。本文就是将相应得参数进行了设置,参会代表 N 名,M 个场次,每场会议 L 个小组,并且要求每个小组得人数基本均衡。本文要以使得尽可能让任意两个来自不同地区得代表之间都有见面沟通得机会为目得,建立数学模型,并设计求解上述分组模型得有效算法.同时,设置一些具体数值对已经建立得模型以及算法进行验算,即、、分别取做3 7、5、5,根据问题 1 所建立得模型以...