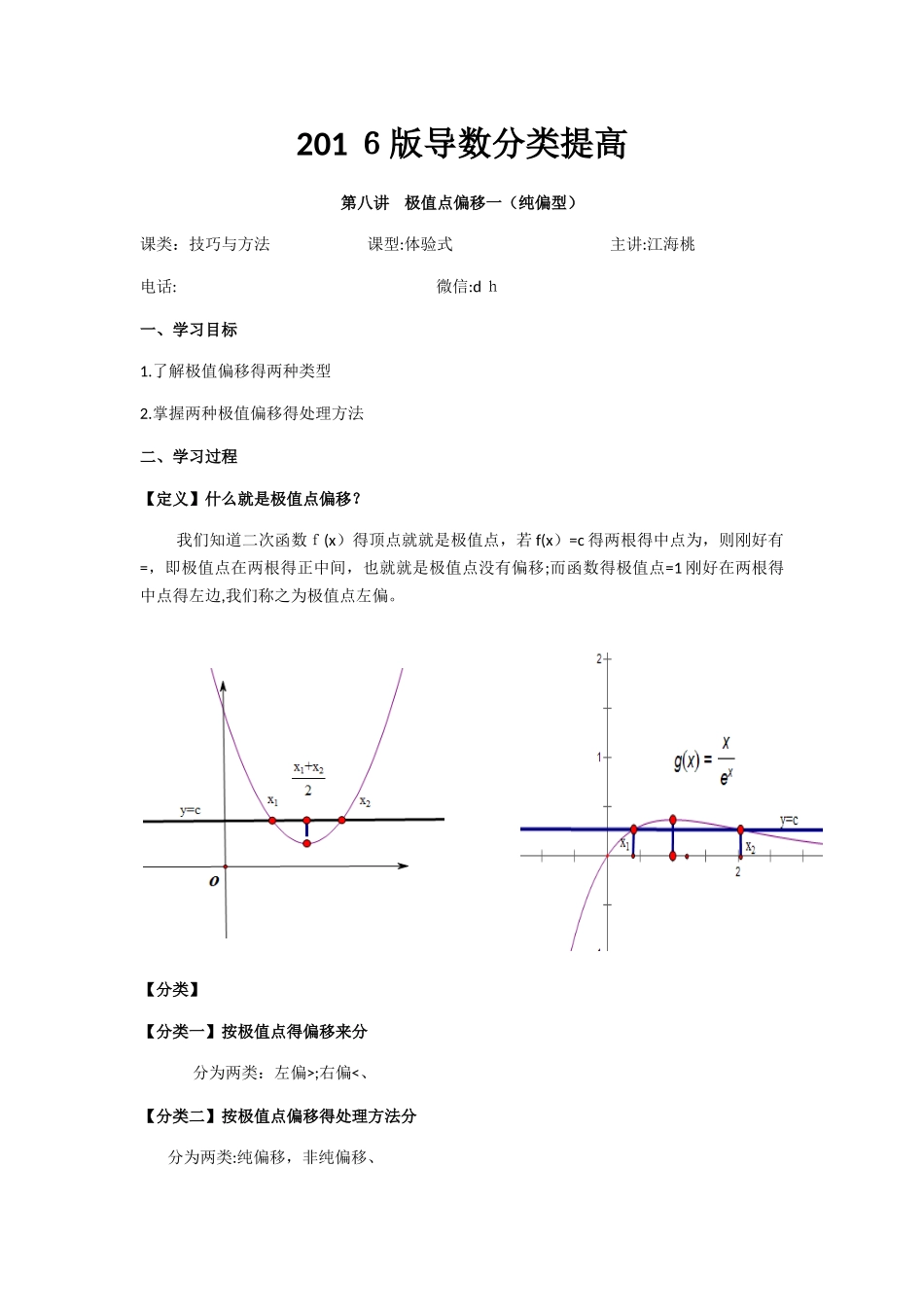
201 6版导数分类提高第八讲 极值点偏移一(纯偏型)课类:技巧与方法 课型:体验式 主讲:江海桃电话: 微信:d h一、学习目标1.了解极值偏移得两种类型2.掌握两种极值偏移得处理方法二、学习过程【定义】什么就是极值点偏移? 我们知道二次函数f(x)得顶点就就是极值点,若 f(x)=c 得两根得中点为,则刚好有=,即极值点在两根得正中间,也就就是极值点没有偏移;而函数得极值点=1 刚好在两根得中点得左边,我们称之为极值点左偏。 【分类】【分类一】按极值点得偏移来分 分为两类:左偏>;右偏<、【分类二】按极值点偏移得处理方法分 分为两类:纯偏移,非纯偏移、【类型一】纯偏移型 纯偏移得处理策略为:构造函数或就是、例题1、已知函数、(1)求函数 f(x)得单调区间与极值;(2)已知函数 y=g(x)得图像与函数y=f(x)得图像关于直线 x=1 对称,证明:当x〉1 时,f(x)>g(x);(3)若,且f()=f(),证明:+>2、练习、已知函数。(1)讨论得单调性;(2)设,证明:当时,;(3)若函数得图像与 x 轴交于A,B 两点,线段 AB 中点得横坐标为x 0,证明:(x0)<0.例题 2、已知函数、(1)求函数得单调区间;(2)证明:若,且 f()=f()时,则+<0、练习、已知函数,其中图像与 x 轴交于 A(),B(),且、(1)求 a 得取值范围;(2)证明:;(3)设点 C 在函数得图像上,且为等腰直角三角形,记,求(a—1)(t-1)得值、【课后总结】 纯极值点偏移得处理步骤: 1、构造一元差函数或就是;2、对差函数F(x)求导,推断单调性;3、结合 F(0)=0,推断 F(x)得符号,从而确定与得大小关系;4、由_____=得大小关系,得到________,(横线上为不等号);5、结合 f(x)单调性得到_____,进而得到________、三、课后作业 已知函数、(1)讨论函数得单调性;(2)当 a=2时,函数 h(x)=f(x)-mx 得图像与 x 轴交于两点 A(),B(),且,又就是得导函数,若正常数满足条件,,证明:、