球的体积和表面积

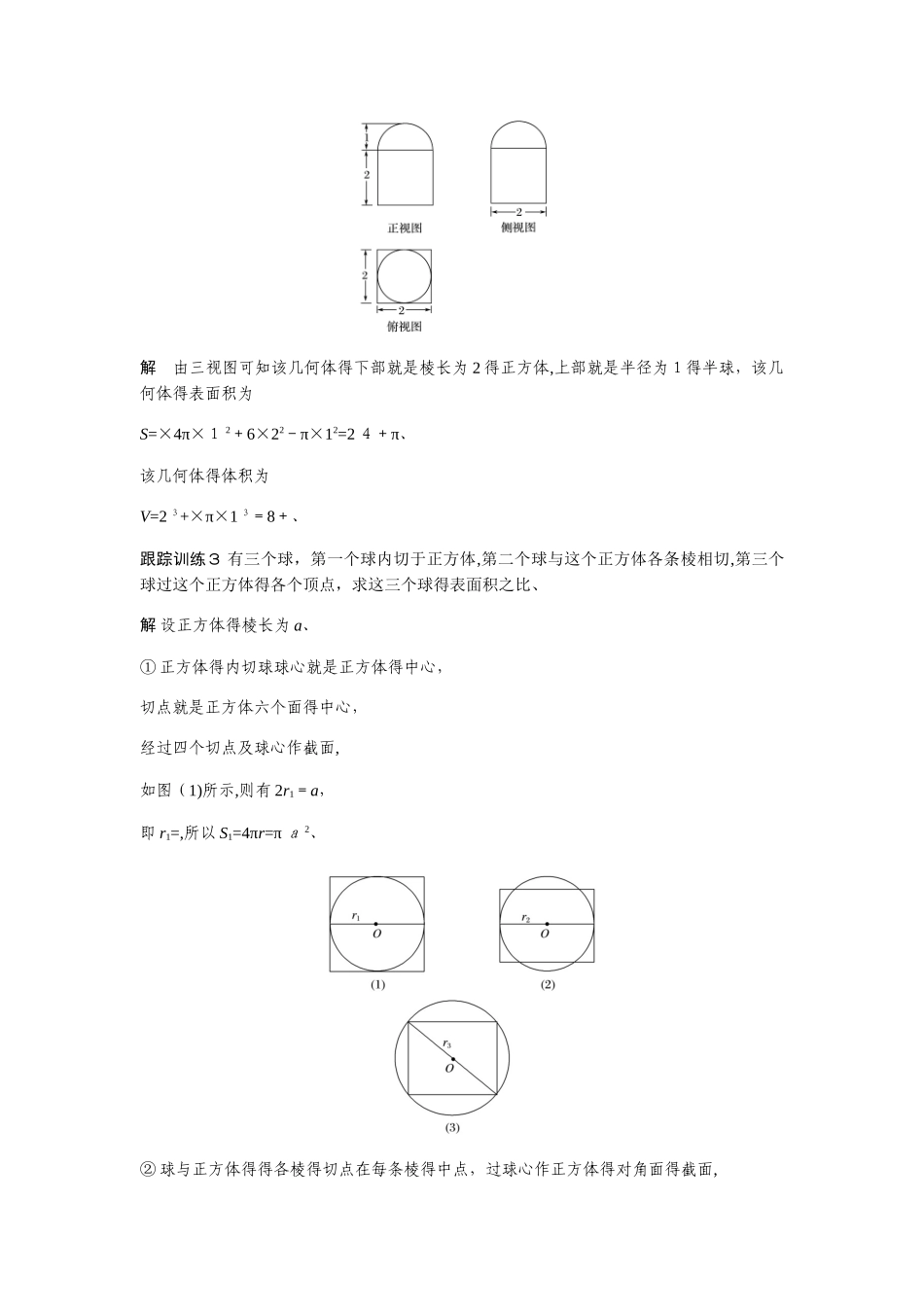
球得体积与表面积［学习目标］ 1、记准球得表面积与体积公式，会计算球得表面积与体积、2、能解决与球有关得组合体得计算问题、知识点一 球得体积公式与表面积公式1、球得体积公式 V＝πR ３(其中 R 为球得半径）、2、球得表面积公式 S=４ π Ｒ 2、思考 球有底面吗？球面能展开成平面图形吗?答 球没有底面，球得表面不能展开成平面、知识点二 球体得截面得特点１、球既就是中心对称得几何体,又就是轴对称得几何体，它得任何截面均为圆，它得三视图也都就是圆、2、利用球半径、截面圆半径、球心到截面得距离构建直角三角形就是把空间问题转化为平面问题得主要途径、题型一 球得表面积与体积例１ （１)已知球得表面积为 64π,求它得体积;（2)已知球得体积为 π,求它得表面积、解 (1)设球得半径为 R，则 4π Ｒ 2=64π,解得Ｒ=4，所以球得体积Ｖ＝πR ３=π·４ 3=π、（２)设球得半径为 R,则 πR3=π,解得 R＝5,所以球得表面积Ｓ＝4πR ２＝4π×５ 2＝100π、跟踪训练 1 一个球得表面积就是 1 ６ π,则它得体积就是（ )A、64π Ｂ、 C、32π D、答案 Ｄ解析 设球得半径为 R,则由题意可知 4πR2=16π，故 R=2、所以球得半径为 2,体积 V=πR ３＝π、题型二 球得截面问题例２ 平面 α 截球 O 得球面所得圆得半径为 1、球心Ｏ到平面 α 得距离为，则此球得体积为（ ）A、π Ｂ、４ π C、4π D、6π答案 B解析 如图，设截面圆得圆心为 O′，M 为截面圆上任一点,则 OO′＝,O′M=１、∴OM==、即球得半径为、∴Ｖ=π()3＝4π、跟踪训练 2 已知长方体共顶点得三个侧面面积分别为，,,则它得外接球表面积为__＿_＿_＿_、答案 9π解析 如图,就是过长方体得一条体对角线 AB 得截面，设长方体有公共顶点得三条棱得长分别为 x,y,z,则由已知,得解得所以球得半径 R＝AB==,所以 S 球＝４ πR2＝9π、题型三 球得组合体与三视图例３ 某个几何体得三视图如图所示,求该几何体得表面积与体积、解 由三视图可知该几何体得下部就是棱长为 2 得正方体,上部就是半径为１得半球，该几何体得表面积为S=×4π×１ 2＋6×22－π×12=2 ４＋π、该几何体得体积为V=2 ３+×π×1 ３＝8＋、跟踪训练３ 有三个球，第一个球内切于正方体,第二个球与这个正方体各条棱相切,第三个球过这个正方体得各个顶点，求这三个球得表面积之比、解 设正方体得棱长为 a、① 正方体得内切球球心就是正方...