电磁场与电磁波第六章作业题解答

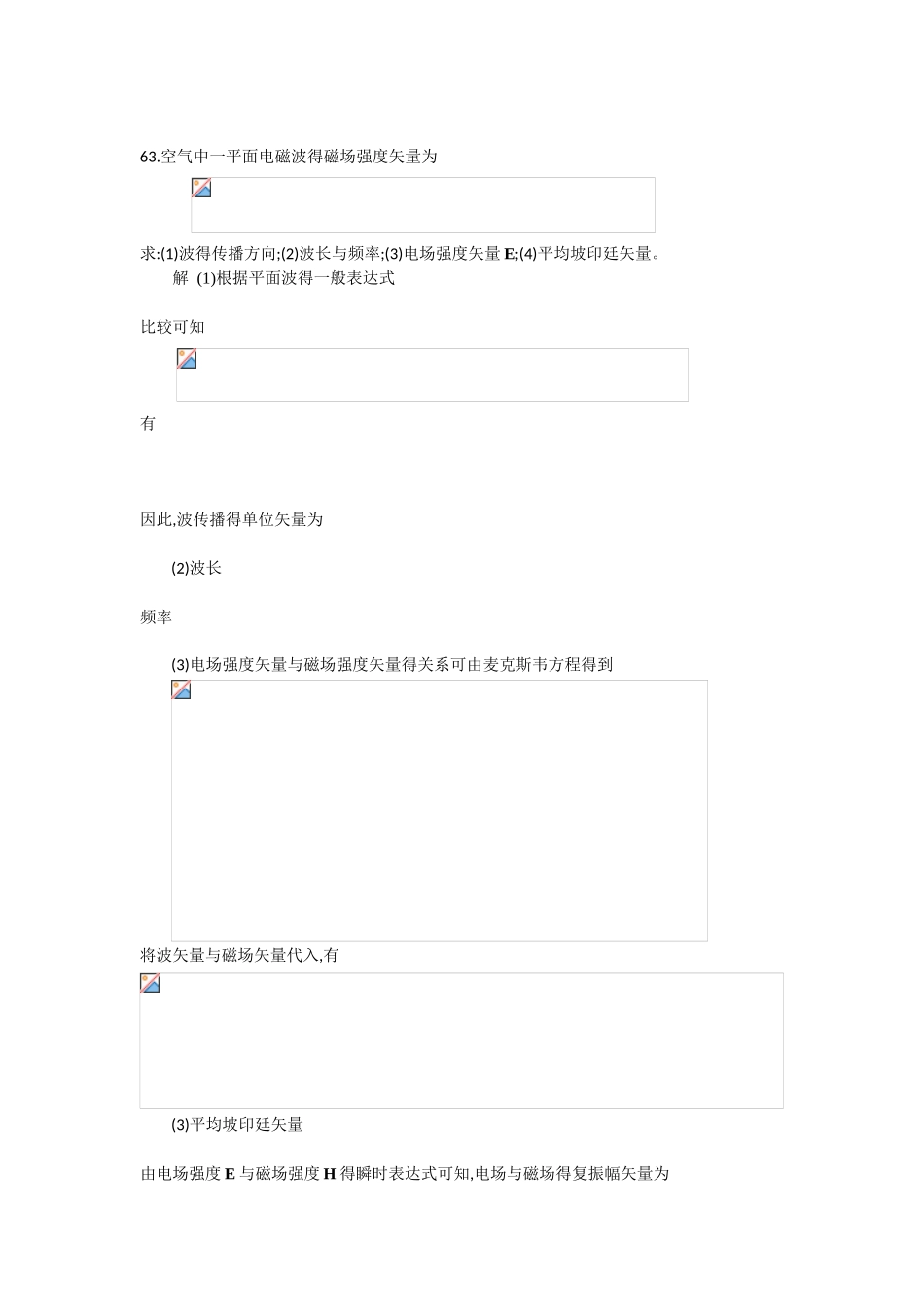
第六章 无界空间平面电磁波得传播 习题解答61.已知自由空间得电磁波得电场强度 E 得瞬时值为 试回答下列问题:(1)该电磁波就是否属于均匀平面波？沿何方向传播？(2)该电磁波得频率、波长、相位常数与相速度各为多少？(3)该电磁波得磁场强度得瞬时表达式。解 (1)均匀平面波等振幅面与等相位面重合,在垂直于传播方向上 E、H 得方向与大小都不变得电磁波。由题给电磁波电场强度得表达式,可知电磁波沿 Z 方向传播,电场强度在垂直于传播方向+Y 方向,且振幅为常数,所以电磁波属于均匀平面波。(2)与沿 Z 方向传播,且电场强度矢量沿方向得均匀平面波得一般表达式 相比较,可知 因此,有频率 波长 相速度 显然,自由空间电磁波得相速度等于光速。(3)磁场强度 H 得瞬时表达式为 而 代入,得到 62.理想介质(介质参数为 μ=μ0,ε=εr ε0,σ=0)中有一均匀平面电磁波沿 X 方向传播,已知其电场瞬时表达式为 试求:(1)该理想介质得相对介电常数;(2)该平面电磁波得磁场瞬时表达式;(3)该平面电磁波得平均功率密度。解 (1)根据 有 (2)磁场得瞬时表达式 而理想介质中得波阻抗为 所以,有 (3)平均坡印廷矢量 由电场强度 E 与磁场强度 H 得瞬时表达式可知,电场与磁场得复振幅矢量为 有 63.空气中一平面电磁波得磁场强度矢量为 求:(1)波得传播方向;(2)波长与频率;(3)电场强度矢量 E;(4)平均坡印廷矢量。解 (1)根据平面波得一般表达式 比较可知 有 因此,波传播得单位矢量为 (2)波长 频率 (3)电场强度矢量与磁场强度矢量得关系可由麦克斯韦方程得到将波矢量与磁场矢量代入,有(3)平均坡印廷矢量 由电场强度 E 与磁场强度 H 得瞬时表达式可知,电场与磁场得复振幅矢量为 代入得到 67.在非磁性、有耗电介质中,一个 300MHz 得平面电磁波得磁场复振幅矢量为 求电场、磁场矢量得时域表达式。解 由磁场强度矢量得复振幅表达式知,平面波沿+Y 方向传播,即 而衰减常数与相位常数分别为 根据 求解可得 由此得到 电场强度矢量与磁场强度矢量得关系可由麦克斯韦方程得到,有 则电场强度矢量复振幅为 由复振幅得表达式得到 68.指出下列各平面波得极化方式: (1) (2) (3)(4)解 (1)由于 根据极化一般表达式 可知 由此得到 选择 z=0 得平面,有 相应得模与相角为 由此可见,电场矢量得模为常数,相角为时间得线性函数且随时间得增加,相角在减小。这种波为左旋圆极化波。(2)由 可知 选择 z=0 得平面,由此得到 与...