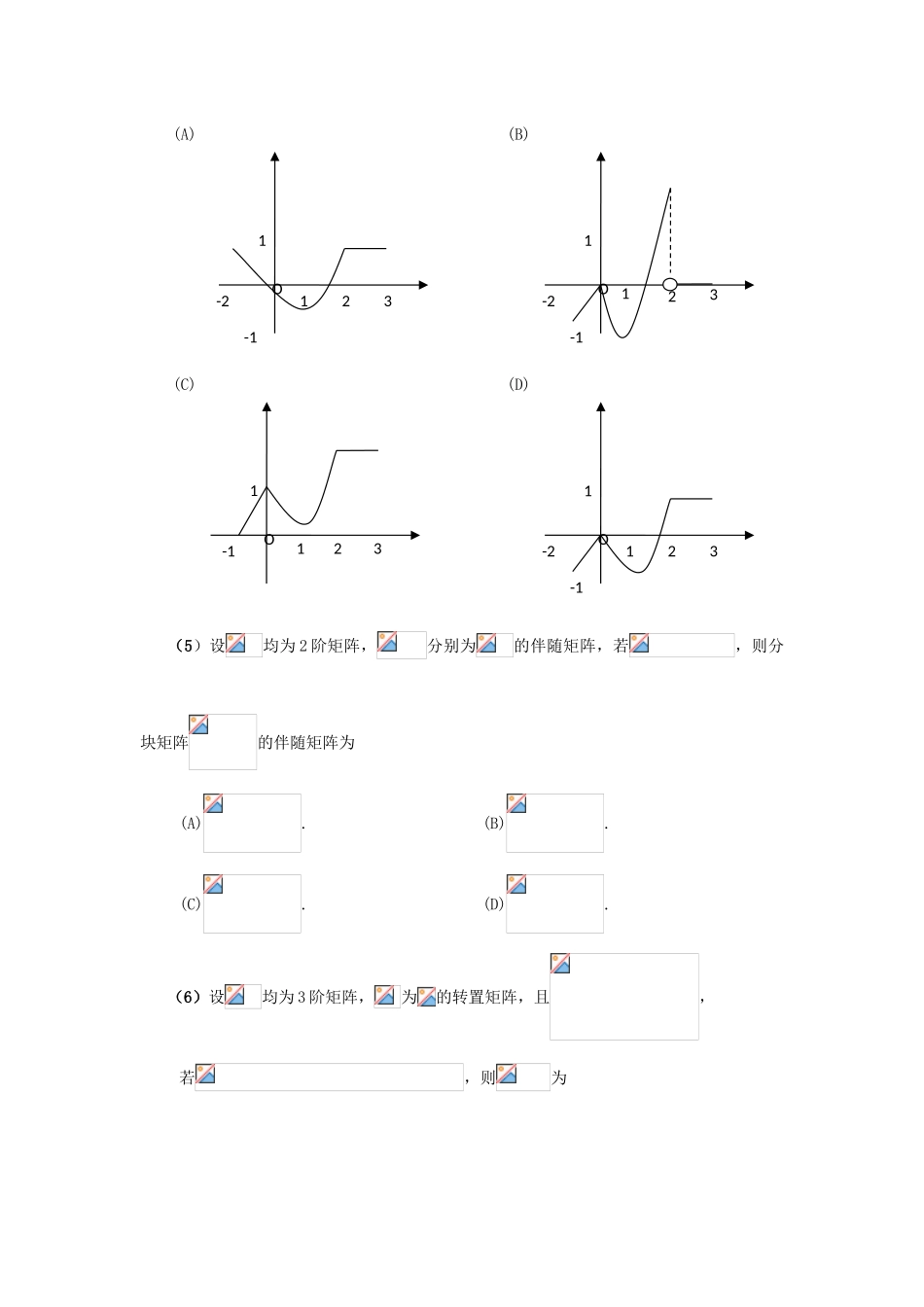
2025 年全国硕士讨论生入学统一考试数学三试题一、选择题:1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数的可去间断点的个数为 (A)1. (B)2. (C)3. (D)无穷多个.(2)当时,与是等价无穷小,则(A),. (B),. (C),. (D),.(3)使不等式成立的的范围是(A).(B). (C). (D).(4)设函数在区间上的图形为则函数的图形为1-2O23-1 1(A) (B)(C) (D)(5)设均为 2 阶矩阵,分别为的伴随矩阵,若,则分块矩阵的伴随矩阵为(A). (B). (C). (D).(6)设均为 3 阶矩阵,为的转置矩阵,且,若,则为O231-2-11O231-2-11O231-11O231-2-11(A). (B). (C). (D).(7)设事件与事件 B 互不相容,则(A). (B). (C). (D).(8)设随机变量与相互独立,且服从标准正态分布,的概率分布为,记为随机变量的分布函数,则函数的间断点个数为(A)0. (B)1. (C)2. (D)3.二、填空题:9~14 小题,每小题 4 分,共 24 分,请将答案写在答题纸指定位置上.(9) .(10)设,则 .(11)幂级数的收敛半径为 .(12)设某产品的需求函数为,其对应价格的弹性,则当需求量为 10000 件时,价格增加 1 元会使产品收益增加 元.(13)设,,若矩阵相似于,则 .(14) 设,,…,为来自二项分布总体的简单随机样本,和分别为样本均值和样本方差,记统计量,则 .三、解答题:15~23 小题,共 94 分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分 9 分)求二元函数的极值.(16)(本题满分 10 分)计算不定积分 .(17)(本题满分 10 分)计算二重积分,其中.(18)(本题满分 11 分)(Ⅰ)证明拉格朗日中值定理,若函数在上连续,在上可导,则,得证.( Ⅱ ) 证 明 : 若 函 数在处 连 续 , 在内 可 导 , 且,则存在,且.(19)(本题满分 10 分)设曲线,其中是可导函数,且.已知曲线与直线及所围成的曲边梯形绕轴旋转一周所得的立体体积值是该曲边梯形面积值的倍,求该曲线的方程.(20)(本题满分 11 分)设,.(Ⅰ)求满足,的所有向量,.(Ⅱ)对(Ⅰ)中的任意向量,,证明,,线性无关.(21)(本题满分 11 分)设二次型.(Ⅰ)求二次型的矩阵的所有特征值.(Ⅱ)若二次型的法律规范形为,求的值.(22)(本题满分 11 分)设二维随机变量的概率密度为(...