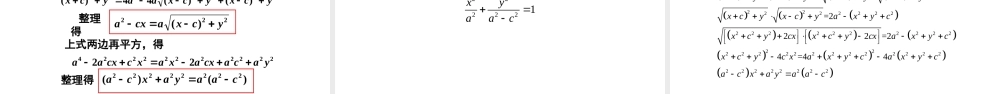椭圆及其标准方程(授课及说课

人教 A 版高中数学选修 2-1椭圆及其标准方程一、情境引入，认识椭圆一、情境引入，认识椭圆运动场跑道是不是椭圆形呢？一、情境引入，认识椭圆鸡蛋是不是椭圆形呢？一、情境引入，认识椭圆椭圆的定义是什么呢？斜截面边缘是椭圆一、情境引入，认识椭圆椭圆的定义是什么呢？斜截面边缘是椭圆一、情境引入，认识椭圆跑道不是椭圆！一、情境引入，认识椭圆鸡蛋不是椭圆！一、情境引入，认识椭圆倾斜杯子水平面边缘是椭圆倾斜放置的杯子，水平面边缘是椭圆吗？一、情境引入，认识椭圆如何判断卫星运行轨迹、桌面边缘是椭圆呢？二、定义椭圆，完善定义椭圆的定义：平面内与两个定点 F1 、 F2 的距离之和等于常数 的点的轨迹是椭圆．实验：（ 1 ）取一条定长的绳子 , 把细绳两端拉开一段距离，分别固定在图板的两点处，并做好标记，套上铅笔，拉紧绳子，移动笔尖，画出的轨迹是什么曲线？二、定义椭圆，完善定义椭圆问题：怎样画出椭圆？二、定义椭圆，完善定义椭圆的定义：平面内与两个定点 F1 、 F2 的距离之和等于常数 的点的轨迹是椭圆．二、定义椭圆，完善定义分析成果问题：若把细绳两端拉直，则画出的轨迹是什么曲线？ 线段. .........二、定义椭圆，完善定义 这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距 .椭圆的定义：平面内与两个定点 F1 、 F2 的距离之和等于常数 的点的轨迹是椭圆． ( 大于 |F1F2|) 大家还记得求曲线方程的一般步骤吗？建系列式设点证明化简三、合理建系，推导方程问题 F1F2如何建系更好？（使方程最简洁）.圆与坐标轴的关系：圆关于 X 、 Y 、原点对称222+=xyr圆方程的最简单形式：Oxy1F2F1F2Fx以两定点、所在直线为 轴，线段y21FF的垂直平分线为 轴，建立直角坐标系 .cFF221)0( c设，、),c(F01 )0,(2 cF则),(yxM为椭圆上的任意一点，)22(ca 又设a2的和等于、M1F2F与的距离M问题：如何化简含两个根式的方程？aMFMFMP221M椭圆上点的集合为aycxycx2)()(2222Oxy1F2FM问题：如何化简含两个根式的方程？aMFMFMP221M椭圆上点的集合为aycxycx2)()(2222整理得222)(ycxacxa上式两边再平方，得2222222222422yacacxaxaxccxaa整理得)()(22222222caayaxca移项平方，得2222222)()(44)(ycxycxaaycx问题：如何化简含两个根式的方程？22222222caayaxca两边同时...