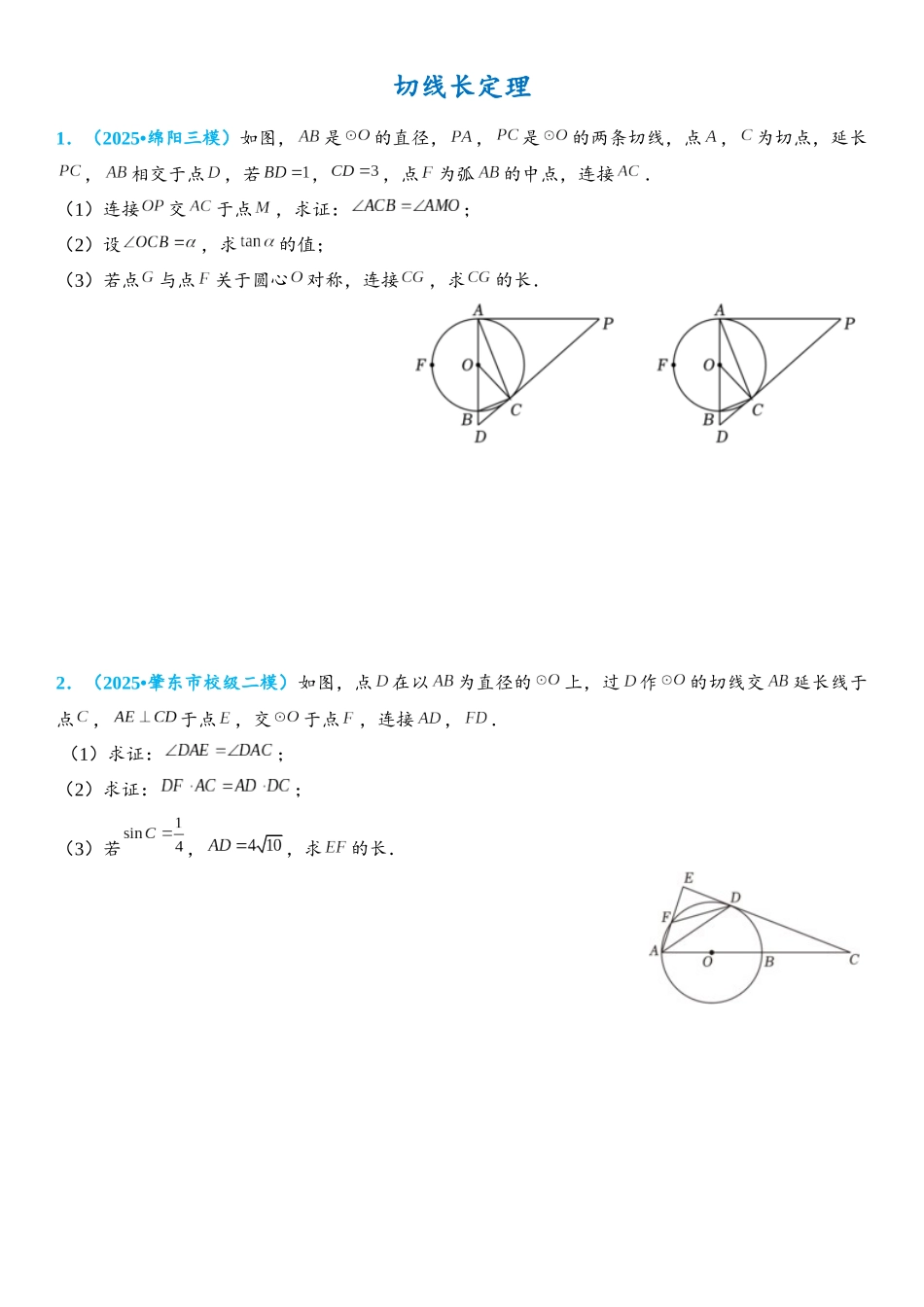
切线长定理1.(2025•绵阳三模)如图,是的直径,,是的两条切线,点,为切点,延长,相交于点,若,,点为弧的中点,连接.(1)连接交于点,求证:;(2)设,求的值;(3)若点与点关于圆心对称,连接,求的长.2.(2025•肇东市校级二模)如图,点在以为直径的上,过作的切线交延长线于点,于点,交于点,连接,. (1)求证:;(2)求证:;(3)若,,求的长.3.(2025•东莞市校级二模)古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.小明决定研究一下圆,如图,是的直径,点是上的一点,延长至点,连接、、,且,过点作于点.(1)求证:是的切线;(2)若,求证:点是的中点;(3)在(2)的条件下,若点是上一点(不与、、重合),求的值.4.(2025•利川市一模)如图,在中,,以为直径的与边交于点,过点作于点.(1)求证:是的切线;(2)若与相交于点,连接,求证:;(3)若,求证:.5.(2024•梁子湖区校级自主招生)等腰直角和如图放置,已知,,的半径为 1,圆心与直线的距离为 5.现以每秒 2 个单位的速度向右移动,同时的边长、又以每秒 0.5 个单位沿、方向增大.(1)当的边边除外)与圆第一次相切时,点移动了多少距离?(2)若在移动的同时,也以每秒 1 个单位的速度向右移动,则从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?(3)在(2)的条件下,是否存在某一时刻,与的公共部分等于的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.6.(2009•肇庆)如图,的直径,和是它的两条切线,切于,交于,交于.设,.(1)求证:;(2)求关于 的关系式;(3)求四边形的面积,并证明:.7.(2007 秋 张家港市期末)•如图,中,,以为直径的与边交于点,过点作的切线,交于点;(1)求证:;(2)若以、、、为顶点的四边形是正方形,的半径为 ,求的面积;(3)若,,求的半径的长.8.(2007•河池)如图 1,已知正方形的边长为,点是的中点,是线段上的一动点不与,重合),以为直径作,过点作的切线交于点,切点为.(1)除正方形的四边和中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线);(2)求四边形的周长;(3)延长,相交于点,如图 2 所示.是否存在点,使?如果存在,试求此时的长;如果不存在,请说明理由.9.(2007•厦门)已知:如图,、是的切线;、是切点;连接、、,(1)若,求的度数;(2)过作...