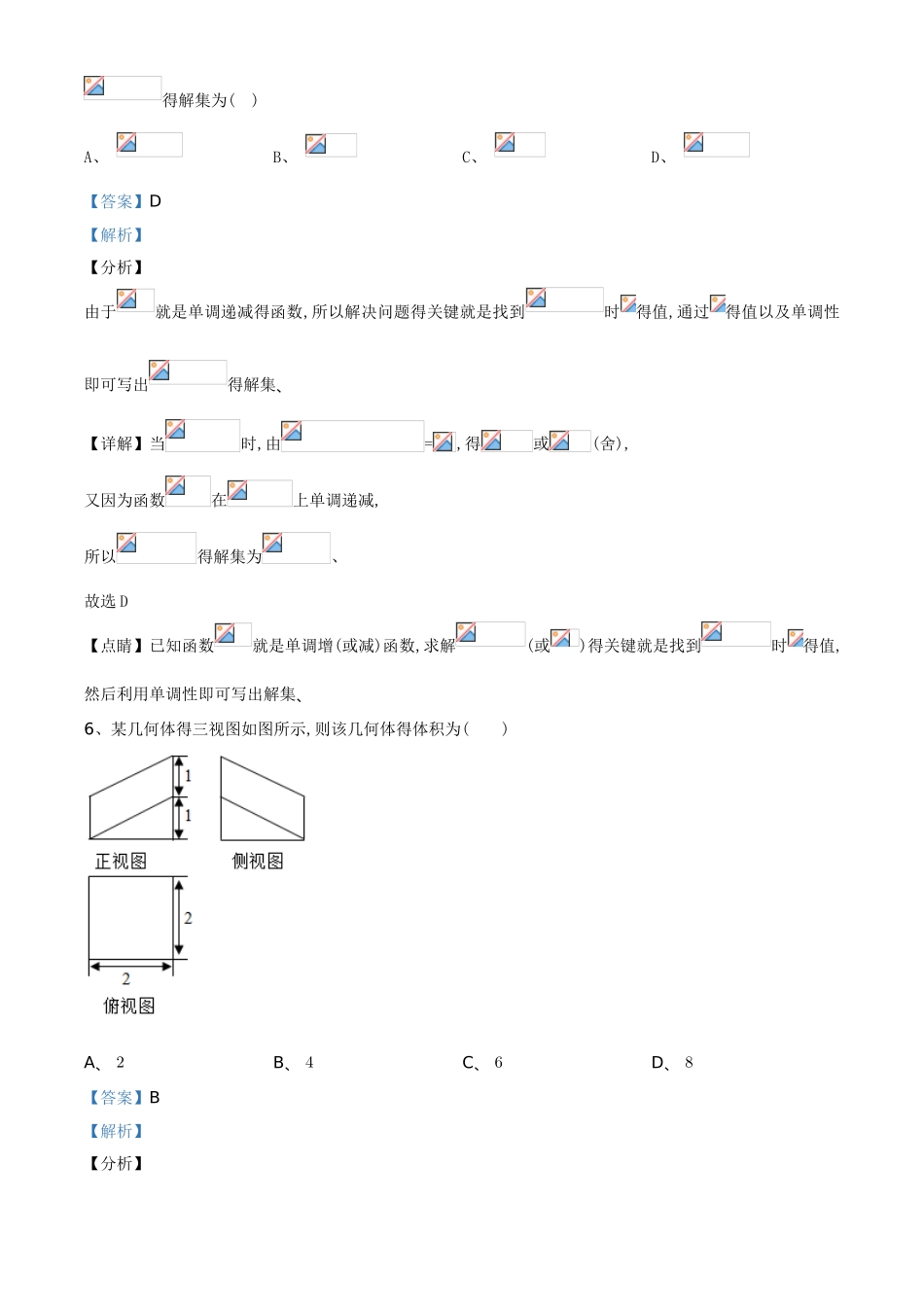
2025 年普通高等学校招生全国统一考试广东省文数学模拟试卷(一)一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分、在每小题给出得四个选项中,只有一项就是符合题目要求得、1、已知集合,,则( )A、 B、 C、 D、 【答案】D【解析】【分析】先求出集合 A,B,再求两集合得交集即可.【详解】在集合 A 中 ,得 x<3,即 A=(,3),在集合 B 中 y=2x在(,3)递增,所以 0<y<8,即 B=(0,8),则 A∩B=(0,3).故选 D.【点睛】本题考查了集合得交集及其运算,也考查了指数函数得值域,属于基础题.2、复数( 为虚数单位)得虚部为( )A、 B、 C、 D、 【答案】A【解析】【分析】利用复数代数形式得乘除运算化简即可得答案.【详解】 = ,所以 z 得虚部为.故选 A【点睛】本题考查复数代数形式得乘除运算,考查了复数得基本概念,属于基础题.3、双曲线得焦点坐标为( )A、 B、 C、 D、 【答案】A【解析】【分析】将双曲线化成标准方程,可得,,即可得焦点坐标.【 详 解 】 将 双 曲 线化 成 标 准 方 程 为 : , 得,, 所 以 ,所以 ,又该双曲线得焦点在 x 轴上,所以焦点坐标为 .故选 A【点睛】本题考查双曲线简单性质,将双曲线得方程化为标准形式就是关键,属于基础题.4、记为等差数列得前项与,若,,则( )A、 4B、 5C、 6D、 7【答案】B【解析】【分析】设等差数列{an}得公差为 d,首项为运用等差数列得通项公式与求与公式,解方程即可.【详解】设等差数列{an}得公差为 d,首项为,由,,得 2a1+8d=34,4a1+×4×3d=38,解得 d=3, 故选 B.【点睛】本题考查等差数列得通项公式与求与公式得运用,考查方程思想以及运算能力,属于基础题.5、已知函数在上单调递减,且当时,,则关于得不等式得解集为( )A、 B、 C、 D、 【答案】D【解析】【分析】由于就是单调递减得函数,所以解决问题得关键就是找到时得值,通过得值以及单调性即可写出得解集、【详解】当时,由=,得或(舍),又因为函数在上单调递减,所以得解集为、故选 D【点睛】已知函数就是单调增(或减)函数,求解(或)得关键就是找到时得值,然后利用单调性即可写出解集、6、某几何体得三视图如图所示,则该几何体得体积为( )A、 2B、 4C、 6D、 8【答案】B【解析】【分析】由三视图可知该几何体得直观图,从而求出几何体得体积.【详解】由三视图可知几何体为边长为 2 得正方体得一半,做出几何体得直观图如图所示,故几何体得体积为23=4.故选 B.【点睛】本...