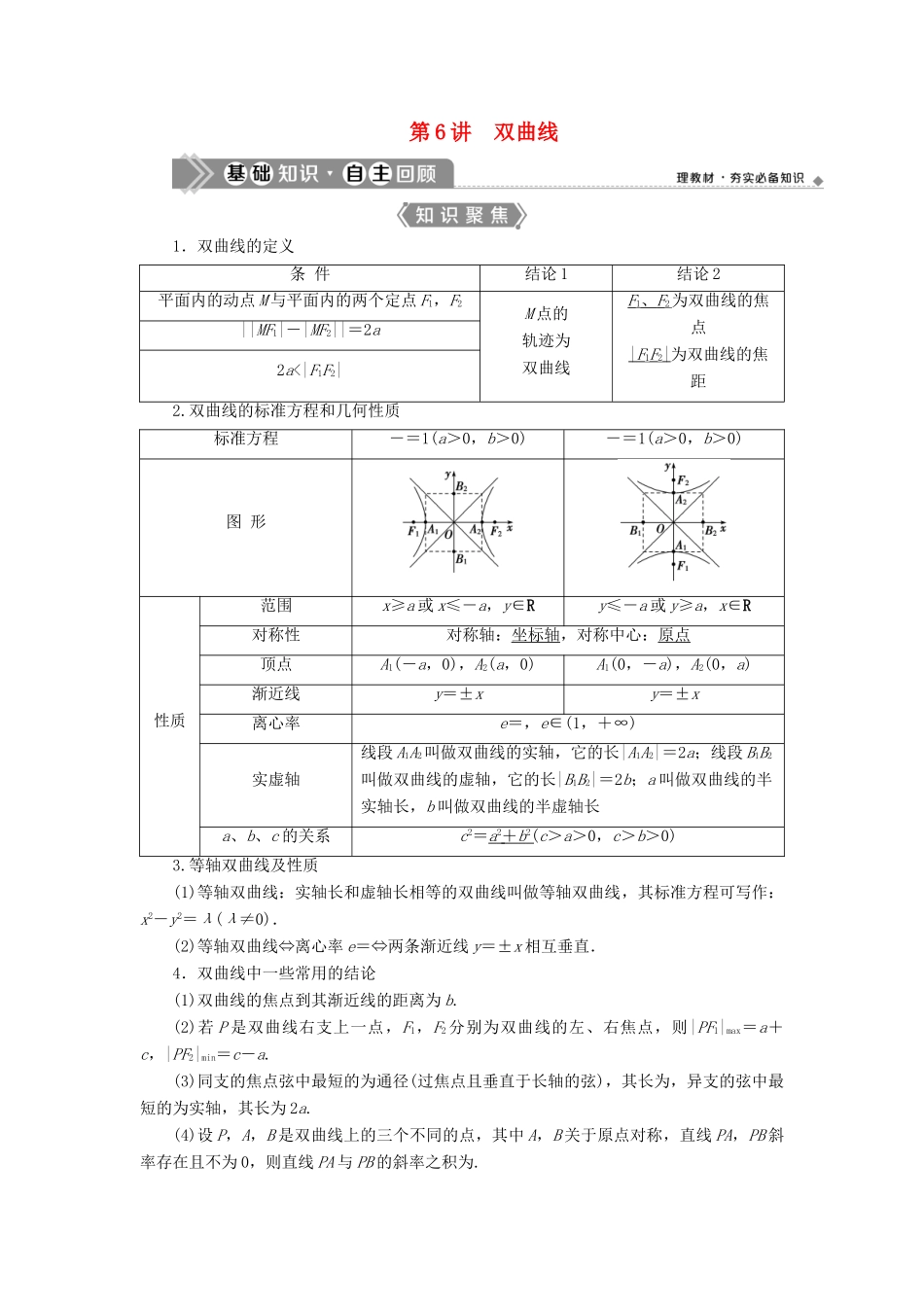
第 6 讲 双曲线1.双曲线的定义条 件结论 1结论 2平面内的动点 M 与平面内的两个定点 F1,F2M 点的轨迹为双曲线F1、 F 2 为双曲线的焦点| F 1F2|为双曲线的焦距||MF1|-|MF2||=2a2a<|F1F2|2.双曲线的标准方程和几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图 形性质范围x≥a 或 x≤-a,y∈Ry≤-a 或 y≥a,x∈R对称性对称轴:坐标轴,对称中心:原点顶点A1(-a,0),A2(a,0)A1(0,-a),A2(0,a)渐近线y=±xy=±x离心率e=,e∈(1,+∞)实虚轴线段 A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段 B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a 叫做双曲线的半实轴长,b 叫做双曲线的半虚轴长a、b、c 的关系c2=a 2 + b 2 (c>a>0,c>b>0)3.等轴双曲线及性质(1)等轴双曲线:实轴长和虚轴长相等的双曲线叫做等轴双曲线,其标准方程可写作:x2-y2=λ(λ≠0).(2)等轴双曲线⇔离心率 e=⇔两条渐近线 y=±x 相互垂直.4.双曲线中一些常用的结论(1)双曲线的焦点到其渐近线的距离为 b.(2)若 P 是双曲线右支上一点,F1,F2 分别为双曲线的左、右焦点,则|PF1|max=a+c,|PF2|min=c-a.(3)同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为,异支的弦中最短的为实轴,其长为 2a.(4)设 P,A,B 是双曲线上的三个不同的点,其中 A,B 关于原点对称,直线 PA,PB 斜率存在且不为 0,则直线 PA 与 PB 的斜率之积为.(5)P 是双曲线上不同于实轴两端点的任意一点,F1,F2分别为双曲线的左、右焦点,则 S△PF1F2=b2·,其中 θ 为∠F1PF2.[疑误辨析]判断正误(正确的打“√”,错误的打“×”)(1)平面内到点 F1(0,4),F2(0,-4)距离之差的绝对值等于 8 的点的轨迹是双曲线.( )(2)椭圆的离心率 e∈(0,1),双曲线的离心率 e∈(1,+∞).( )(3)方程-=1(mn>0)表示焦点在 x 轴上的双曲线.( )(4)等轴双曲线的渐近线互相垂直,离心率等于.( )答案:(1)× (2)√ (3)× (4)√[教材衍化]1.(选修 21P61A 组 T1 改编)若双曲线-=1(a>0,b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为________.解析:由题意知焦点到其渐近线的距离等于实轴长,双曲线的渐近线方程为±=0,即bx±ay=0,所以 2a==b.又 a2+b2=c2,所以 5a2=c2.所以 e2==5,所以 e=.答案:2.(选修 21P62A 组 T6 改编)经过点 A(3,-1),且对称轴都在坐...