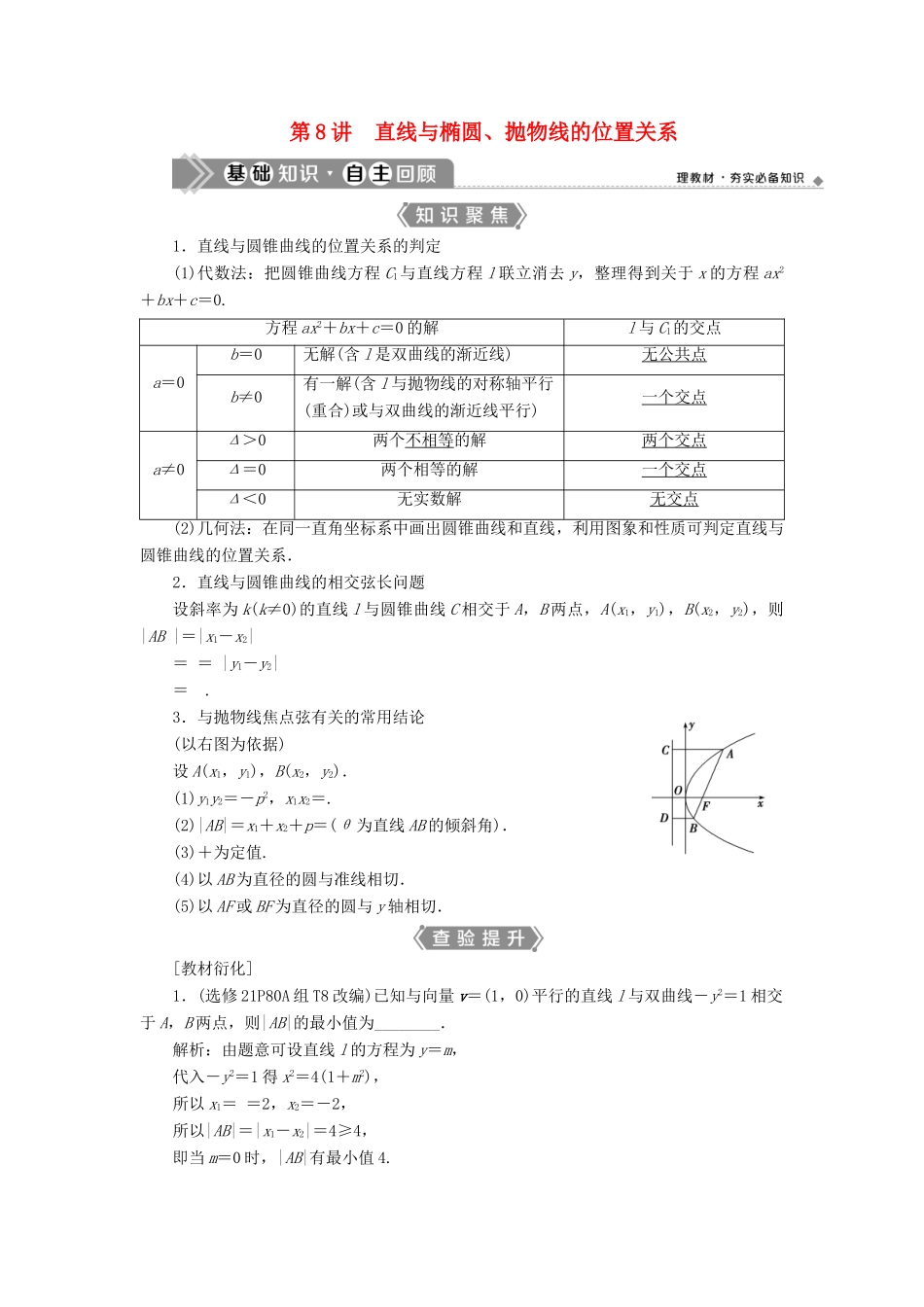
第 8 讲 直线与椭圆、抛物线的位置关系1.直线与圆锥曲线的位置关系的判定(1)代数法:把圆锥曲线方程 C1与直线方程 l 联立消去 y,整理得到关于 x 的方程 ax2+bx+c=0.方程 ax2+bx+c=0 的解l 与 C1的交点a=0b=0无解(含 l 是双曲线的渐近线)无公共点b≠0有一解(含 l 与抛物线的对称轴平行(重合)或与双曲线的渐近线平行)一个交点a≠0Δ>0两个不相等的解两个交点Δ=0两个相等的解一个交点Δ<0无实数解无交点(2)几何法:在同一直角坐标系中画出圆锥曲线和直线,利用图象和性质可判定直线与圆锥曲线的位置关系.2.直线与圆锥曲线的相交弦长问题设斜率为 k(k≠0)的直线 l 与圆锥曲线 C 相交于 A,B 两点,A(x1,y1),B(x2,y2),则|AB |=|x1-x2|= = |y1-y2|= .3.与抛物线焦点弦有关的常用结论(以右图为依据)设 A(x1,y1),B(x2,y2).(1)y1y2=-p2,x1x2=.(2)|AB|=x1+x2+p=(θ 为直线 AB 的倾斜角).(3)+为定值.(4)以 AB 为直径的圆与准线相切.(5)以 AF 或 BF 为直径的圆与 y 轴相切.[教材衍化]1.(选修 21P80A 组 T8 改编)已知与向量 v=(1,0)平行的直线 l 与双曲线-y2=1 相交于 A,B 两点,则|AB|的最小值为________.解析:由题意可设直线 l 的方程为 y=m,代入-y2=1 得 x2=4(1+m2),所以 x1= =2,x2=-2,所以|AB|=|x1-x2|=4≥4,即当 m=0 时,|AB|有最小值 4.答案:42 . ( 选 修 21P72 练 习 T4 改 编 ) 过 抛 物 线 y2 = 4x 的 焦 点 的 直 线 l 交 抛 物 线 于P(x1,y1),Q(x2,y2)两点,如果 x1+x2=6,则|PQ|=________.解析:抛物线 y2=4x 的焦点为 F(1,0),准线方程为 x=-1.根据题意可得,|PQ|=|PF|+|QF|=x1+1+x2+1=x1+x2+2=8.答案:8[易错纠偏](1)没有发现直线过定点,导致运算量偏大;(2)不会用函数法解最值问题;(3)错用双曲线的几何性质.1.直线 y=kx-k+1 与椭圆+=1 的位置关系为( )A.相交 B.相切C.相离 D.不确定解析:选 A.直线 y=kx-k+1=k(x-1)+1 恒过定点(1,1),又点(1,1)在椭圆内部,故直线与椭圆相交.故选 A.2.如图,两条距离为 4 的直线都与 y 轴平行,它们与抛物线 y2=-2px(0<p<14)和圆(x-4)2+y2=9 分别交于 A,B 和 C,D,且抛物线的准线与圆相切,则当|AB|·|CD|取得最大值时,直线 AB 的方程为________.解析...