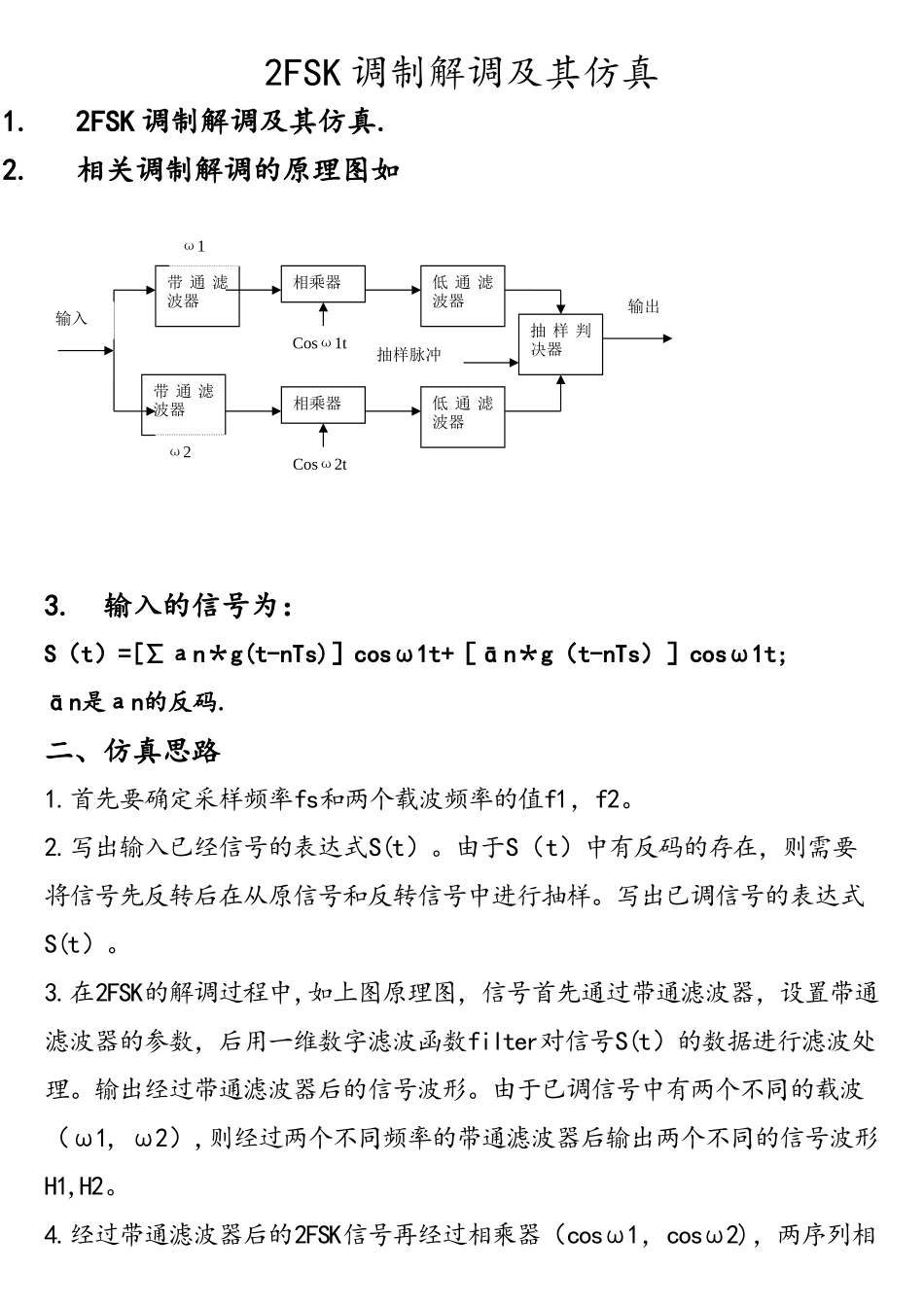
2FSK 调制解调及其仿真1. 2FSK 调制解调及其仿真.2. 相关调制解调的原理图如3. 输入的信号为:S(t)=[∑аn*g(t-nTs)]cosω1t+[ān*g(t-nTs)]cosω1t; ān是аn的反码.二、仿真思路1.首先要确定采样频率fs和两个载波频率的值f1,f2。2.写出输入已经信号的表达式S(t)。由于S(t)中有反码的存在,则需要将信号先反转后在从原信号和反转信号中进行抽样。写出已调信号的表达式S(t)。3.在2FSK的解调过程中,如上图原理图,信号首先通过带通滤波器,设置带通滤波器的参数,后用一维数字滤波函数filter对信号S(t)的数据进行滤波处理。输出经过带通滤波器后的信号波形。由于已调信号中有两个不同的载波(ω1, ω2),则经过两个不同频率的带通滤波器后输出两个不同的信号波形H1,H2。4.经过带通滤波器后的2FSK信号再经过相乘器(cosω1,cosω2),两序列相带 通 滤波器带 通 滤波器相乘器相乘器低 通 滤波器低 通 滤波器抽 样 判决器Cosω1tCosω2tω1ω2抽样脉冲输出输入乘的MATLAB表达式y=x1.*x2 → SW=Hn.*Hn ,输出得到相乘后的两个不同的2FSK波形h1,h2。5.经过相乘器输出的波形再通过低通滤波器,设置低通滤波器的参数,用一维数字滤波韩式filter对信号的数据进行新的一轮的滤波处理。输出经过低通滤波器后的两个波形(sw1,sw2)。6.将信号sw1和sw2同时经过抽样判决器,分别输出st1,st2。其抽样判决器输出的波形为最后的输出波形st。对抽样判决器经定义一个时间变量长度i,当st1(i)>=st2(i)时,则st=0,否则st=st2(i).其中st=st1+st2。三、仿真程序程序如下:fs=2000; %采样频率dt=1/fs;f1=20;f2=120; %两个信号的频率a=round(rand(1,10)); %随机信号g1=ag2=~a; %信号反转,和g1反向g11=(ones(1,2000))'*g1; %抽样g1a=g11(:)';g21=(ones(1,2000))’*g2;g2a=g21(:)’;t=0:dt:10-dt;t1=length(t);fsk1=g1a.*cos(2*pi*f1。*t);fsk2=g2a。*cos(2*pi*f2.*t);fsk=fsk1+fsk2; %产生的信号no=0。01*randn(1,t1); %噪声sn=fsk+no;subplot(311);plot(t,no); %噪声波形title('噪声波形')ylabel(’幅度’)subplot(312);plot(t,fsk);title('产生的波形')ylabel('幅度’)subplot(313);plot(t,sn);title(’将要通过滤波器的波形')ylabel('幅度的大小')xlabel(’t')figure(2) %FSK解调 b1=fir1(101,[10/800 20/800]);b2=fir1(101,[90/800 110/800]); %设...