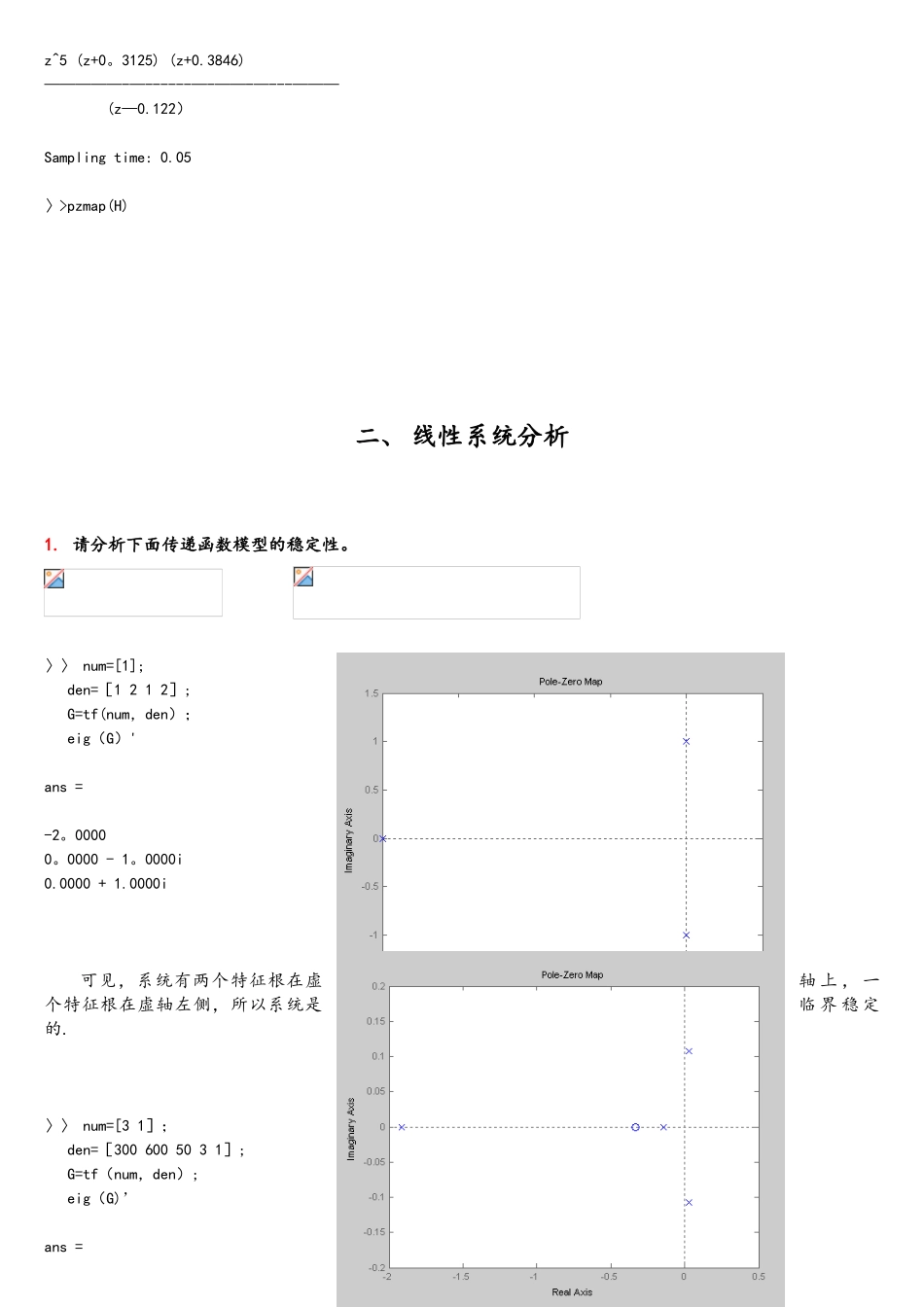
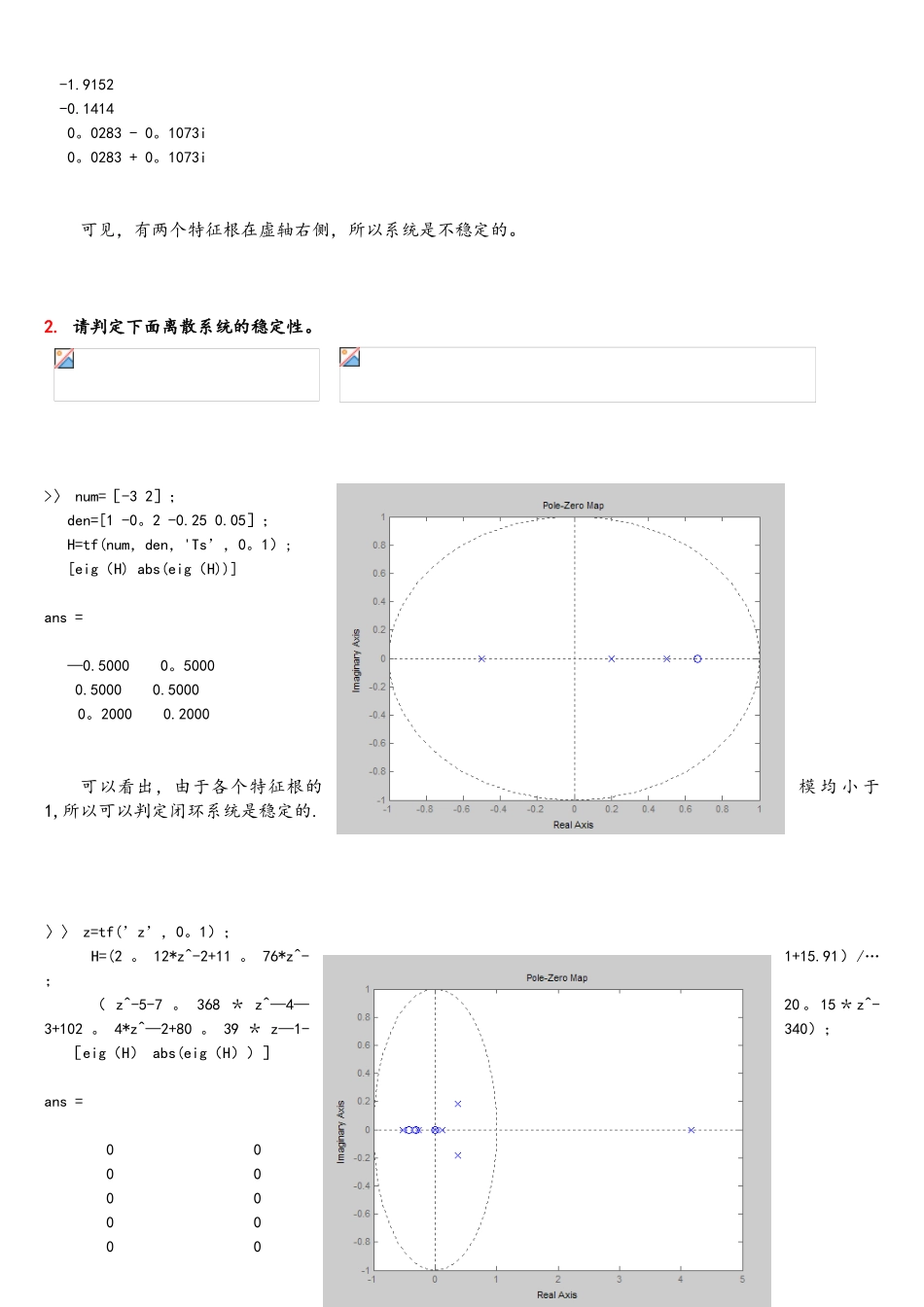
一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到 matlab 环境。 ,T=0.1s>> s=tf(’s'); G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5)); G Transfer function: s^3 + 4 s + 2———————--—-—-———-——————-—------—-——-——---———-———---——-s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3〉〉 num=[1 0 0。56]; den=conv([1 -1],[1 —0。2 0。99]); H=tf(num,den,’Ts’,0。1) Transfer function: z^2 + 0.56————-——--—————---—————-—-—--—z^3 - 1.2 z^2 + 1。19 z — 0。992.请将下面的零极点模型输入到 matlab 环境。请求出上述模型的零极点,并绘制其位置。 ,T=0.05s>>z=[-1—j —1+j]; p=[0 0 -5 -6 —j j]; G=zpk(z,p,8) Zero/pole/gain: 8 (s^2 + 2s + 2)——--—-—--———---——-——-—---—s^2 (s+5) (s+6) (s^2 + 1)〉〉pzmap(G)>> z=[0 0 0 0 0 -1/3。2 -1/2。6]; p=[1/8。2]; H=zpk(z,p,1,’Ts',0.05) Zero/pole/gain:z^5 (z+0。3125) (z+0.3846)—————-—------—-——-—---——— (z—0.122) Sampling time: 0.05〉>pzmap(H)二、 线性系统分析1. 请分析下面传递函数模型的稳定性。 〉〉 num=[1];den=[1 2 1 2];G=tf(num,den);eig(G)'ans =-2。0000 0。0000 - 1。0000i 0.0000 + 1.0000i可见,系统有两个特征根在虚轴 上 , 一个特征根在虚轴左侧,所以系统是临 界 稳 定的.〉〉 num=[3 1];den=[300 600 50 3 1];G=tf(num,den);eig(G)’ans = -1.9152 -0.14140。0283 - 0。1073i 0。0283 + 0。1073i可见,有两个特征根在虚轴右侧,所以系统是不稳定的。2. 请判定下面离散系统的稳定性。 >〉 num=[-3 2]; den=[1 -0。2 -0.25 0.05]; H=tf(num,den,'Ts’,0。1); [eig(H) abs(eig(H))] ans = —0.5000 0。5000 0.5000 0.50000。2000 0.2000可以看出,由于各个特征根的模 均 小 于1,所以可以判定闭环系统是稳定的.〉〉 z=tf(’z’,0。1); H=(2 。 12*z^-2+11 。 76*z^-1+15.91)/…;( z^-5-7 。 368 * z^—4—20 。 15 * z^-3+102 。 4*z^—2+80 。 39 * z—1-340); [eig(H) abs(eig(H))] a...