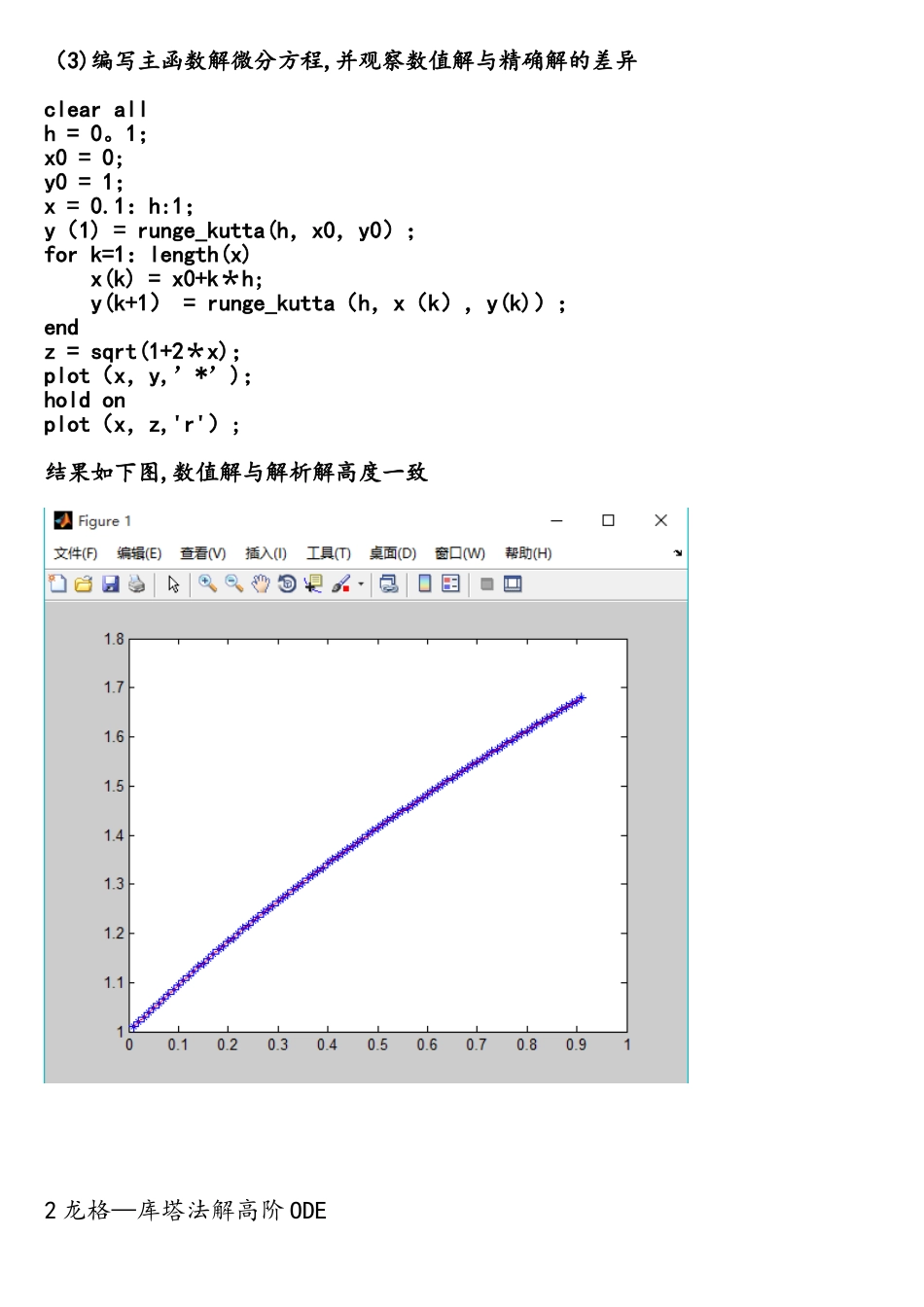
龙格—库塔方法是一种经典方法,具有很高的精度,它间接的利用了泰勒级数展开,避开了高阶偏导数的计算。此处以最为经典的四级四阶龙格-库塔方法为例,计算格式如下 1 龙格—库塔法解一阶 ODE对于形如 的一阶 ODE 初值问题,可以直接套用公式,如今可以借助计算机方便的进行计算,下面给出一个实例 取步长 h=0。1,此处由数学知识可得该方程的精确解为 。在这里利用 MATLAB 编程,计算数值解并与精确解相比,代码如下:(1)写出微分方程,便于调用和修改function val = odefun( x,y ) val = y—2*x/y; end(2)编写 runge-kutta 方法的函数代码function y = runge_kutta( h,x0,y0 )k1 = odefun(x0,y0);k2 = odefun(x0+h/2,y0+h/2*k1);k3 = odefun(x0+h/2,y0+h/2*k2);k4 = odefun(x0+h,y0+h*k3); y = y0+h*(k1+2*k2+2*k3+k4)/6; end(3)编写主函数解微分方程,并观察数值解与精确解的差异clear allh = 0。1;x0 = 0;y0 = 1;x = 0.1:h:1;y(1) = runge_kutta(h,x0,y0);for k=1:length(x) x(k) = x0+k*h; y(k+1) = runge_kutta(h,x(k),y(k));endz = sqrt(1+2*x);plot(x,y,’*’);hold onplot(x,z,'r');结果如下图,数值解与解析解高度一致2 龙格—库塔法解高阶 ODE对于高阶 ODE 来说,通用的方法是将高阶方程通过引入新的变量降阶为一阶方程组,此处仍以一个实例进行说明。 这是一个二阶 ODE,描述的是一个物体的有阻尼振动情况。初始条件为 ,将方程降阶,引入一个向量型变量 Y故有 记则至此,二阶方程降阶为一阶方程组。值得注意的是此时再用龙格-库塔法进行求解时,代入的将是一个 Y 向量。同样利用 MATLAB 进行计算,步长 h=0。05,时间周期为[0,20].(1) 编写 ODE 函数function Y = odefun1( ~,Y0 )% 此处Y0为一个列向量,因为时间t未显含在一阶方程组中% 所以ode函数的第一个参数为空,要根据具体情况而定。Y = [Y0(2); (2000-200*Y0(2)-750*Y0(1))/500;];end(2)编写 runge—kutta 函数function Y = rkfa( h,t0,Y0 )k1 = odefun1(t0,Y0);k2 = odefun1(t0+h/2,Y0+h/2*k1);k3 = odefun1(t0+h/2,Y0+h/2*k2);k4 = odefun1(t0+h,Y0+h*k3);Y = Y0+h*(k1+2*k2+2*k3+k4)/6;end(3)编写主函数clear allh = 0。05;t = 0。05:h:20;t0 = 0;Y0 = [0; 0];%初值Y = cell(1,length(t));Y{1} = rkfa( h,t0,Y0 );z = zeros(2,length(t));for k=1:length(t) Y{k+1} = rkfa( h,t0,Y{k}); z(1,k) = Y{k}(1);z(2,k) = Y{k}(2);endplot(t,z(1,:),'r');%位移y的图像 hold onplot(t,z(2,:));%速度y’的图像求解结果如下图