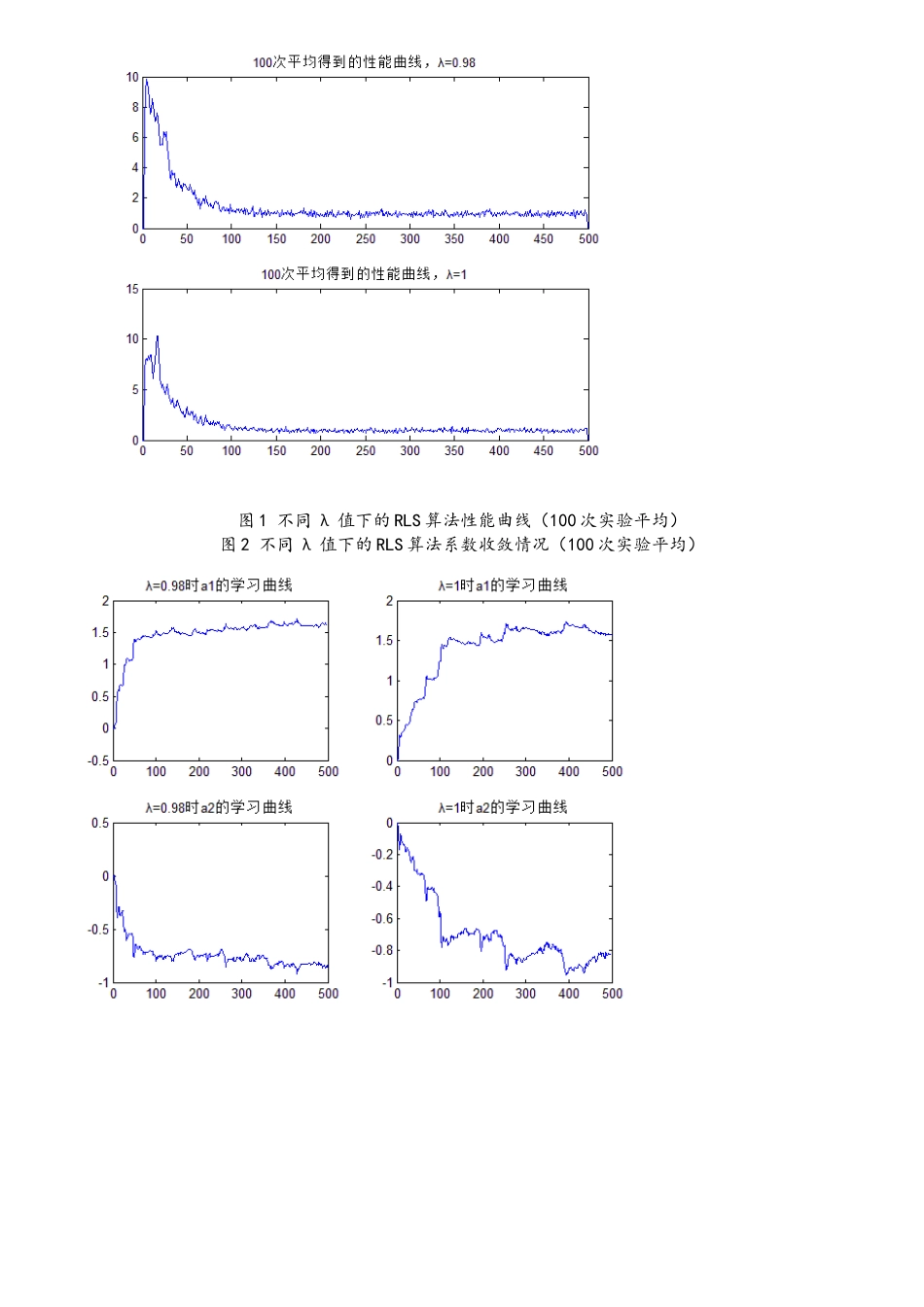
RLS 自适应滤波器仿真作业工程 1 班220250820 王子豪1。 步骤1)令 hM(—1)=0,计算滤波器的输出 d(n)=XMT=hM(n-1);2)计算误差值 eM(n)=d(n)—d(n,n—1);3)计算 Kalman 增益向量 KM(n);4)更新矩阵的逆 RM—1(N)=PM(N);5)计算 hM(n)=hM(n-1)+KM(n)eM(n);2. 仿真RLS 中取 T (—1)=10,λ=1 及 λ= 0.98;信号源 x(n)与之前 LMS 算法仿真不变,对自适应滤波器采纳 RLS 算法。通过对比不同遗忘因子 λ 的情况下 RLS 的误差收敛情况.取 λ=0.98 和 λ=1 两种情况下的性能曲线如图 1 所示。其系数收敛情况如图 2 所示.图 1 不同 λ 值下的 RLS 算法性能曲线(100 次实验平均)图 2 不同 λ 值下的 RLS 算法系数收敛情况(100 次实验平均)3. 结果分析RLS 算法在算法的稳态阶段、即算法的后期收敛阶段其性能和 LMS 算法相差不明显。但在算法的前期收敛段,RLS 算法的收敛速度要明显高于 LMS 算法。但是 RLS 算法复杂度高,计算量比较大。遗忘因子 λ 越小,系统的跟踪能力越强,同时对噪声越敏感;其值越大,系统跟踪能力减弱,但对噪声不敏感,收敛时估量误差也越小。4. Matlab 程序clear;clc;N=2048; %信号的取样点数M=2;%滤波器抽头的个数iter=500;%迭代次数%初始化X_A=zeros(M,1);%X 数据向量y=zeros(1,N);%预测输出err=zeros(1,iter);%误差向量errp=zeros(1,iter);%平均误差wR=zeros(M,iter); %每一行代表一次迭代滤波器的 M 个抽头参数T=eye(M,M)*10; %RLS 算法下 T 参数的初始化,T 初始值为 10X=zeros(1,M);lamuta=0.98 ; %遗忘因子 for j=1:100 ex=randn(1,N);%噪声信号 e(n) x=filter(1,[1,-1。6,0.8],ex);%经过系统 H(Z)之后输出 x d=x;%参考信号 for k=(M+1):iter—1 X=x(k—1:—1:k—M)'; K=(T*X)/(lamuta+X'*T*X); %k 时刻增益值 e1=x(k)—wR(:,k-1)’*X; wR(:,k)=wR(:,k-1)+K*e1; %k 时刻权值 y(k)=wR(:,k)’*X; err(k)=x(k)—y(k); T=(T-K*X'*T)/lamuta; %k 时刻的维纳解 end errp=errp+err。^2;enderrp=errp/100;figure(1);subplot(2,1,i);plot(errp) ;title([’100 次平均得到的性能曲线,λ=’,num2str(lamuta_v(i))]) ;learn1=wR(1,1:iter—1);learn2=wR(2,1:iter-1);figure(2);subplot(1,2,1;plot(learn1);title('λ=0。98’时 a1 的学习曲线');subplot(1,2,2);plot(learn2);title('λ=0。98 时 a2 的学习曲线');