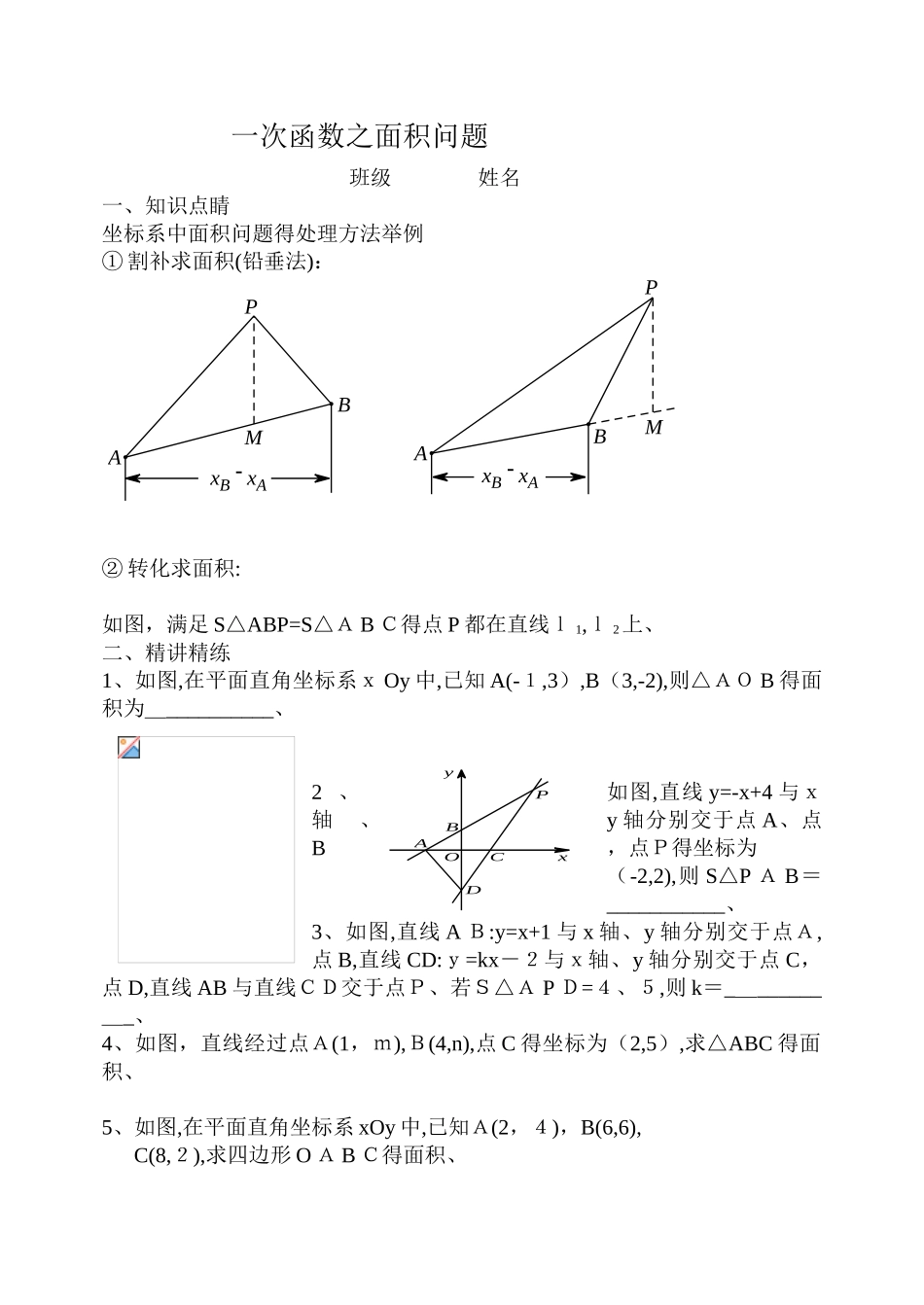
一次函数之面积问题 班级 姓名 一、知识点睛坐标系中面积问题得处理方法举例① 割补求面积(铅垂法):xB - xAxB - xABAMPPMAB ② 转化求面积:如图,满足 S△ABP=S△A B C得点 P 都在直线l 1,l 2上、二、精讲精练1、如图,在平面直角坐标系x Oy 中,已知 A(-1,3),B(3,-2),则△AO B 得面积为___________、2 、如图,直线 y=-x+4 与x轴、y 轴分别交于点 A、点B,点P得坐标为(-2,2),则 S△P A B=___________、3、如图,直线 A B:y=x+1 与 x 轴、y 轴分别交于点A,点 B,直线 CD:y=kx-2与x轴、y 轴分别交于点 C,点 D,直线 AB 与直线CD交于点P、若S△A P D=4、5,则 k=__________、4、如图,直线经过点A(1,m),B(4,n),点 C 得坐标为(2,5),求△ABC 得面积、5、如图,在平面直角坐标系 xOy 中,已知A(2,4),B(6,6),C(8,2),求四边形 O A B C得面积、PDOByACx6、如图,直线与 x 轴、y 轴分别交于 A,B 两点,点C得坐标为(1,2),坐标轴上就就是否存在点P,使 S△ABP=S△A B C?若存在,求出点 P 得坐标;若不存在,请说明理由、7 、 已 知 直 线 与 x 轴 、 y 轴 分 别 交 于A,B 两点,以A为直角顶点,线段 AB 为腰在第一象限内作等腰 Rt△AB C,P为直线 x=1上得动点,且△AB P得面积与△ABC 得面积相等、(1)求△ABC 得面积;(2)求点P得坐标、8、如图,点 A 在直线l 1:y=2x 上,过 A 作 AB⊥x 轴,交直线l2:于点 B、若 AB=3,求 A 点得坐标。9如图,在平面直角坐标系 xOy 中,直线与交于点 A,两直线与 x 轴分别交于点 B 与点 C,D就就是线段 AC 上得一点、点 E 在直线AB上,且 D E∥OA,DE=OA,求点 E 得坐标。、l2l1xyOBAyxEODCBA