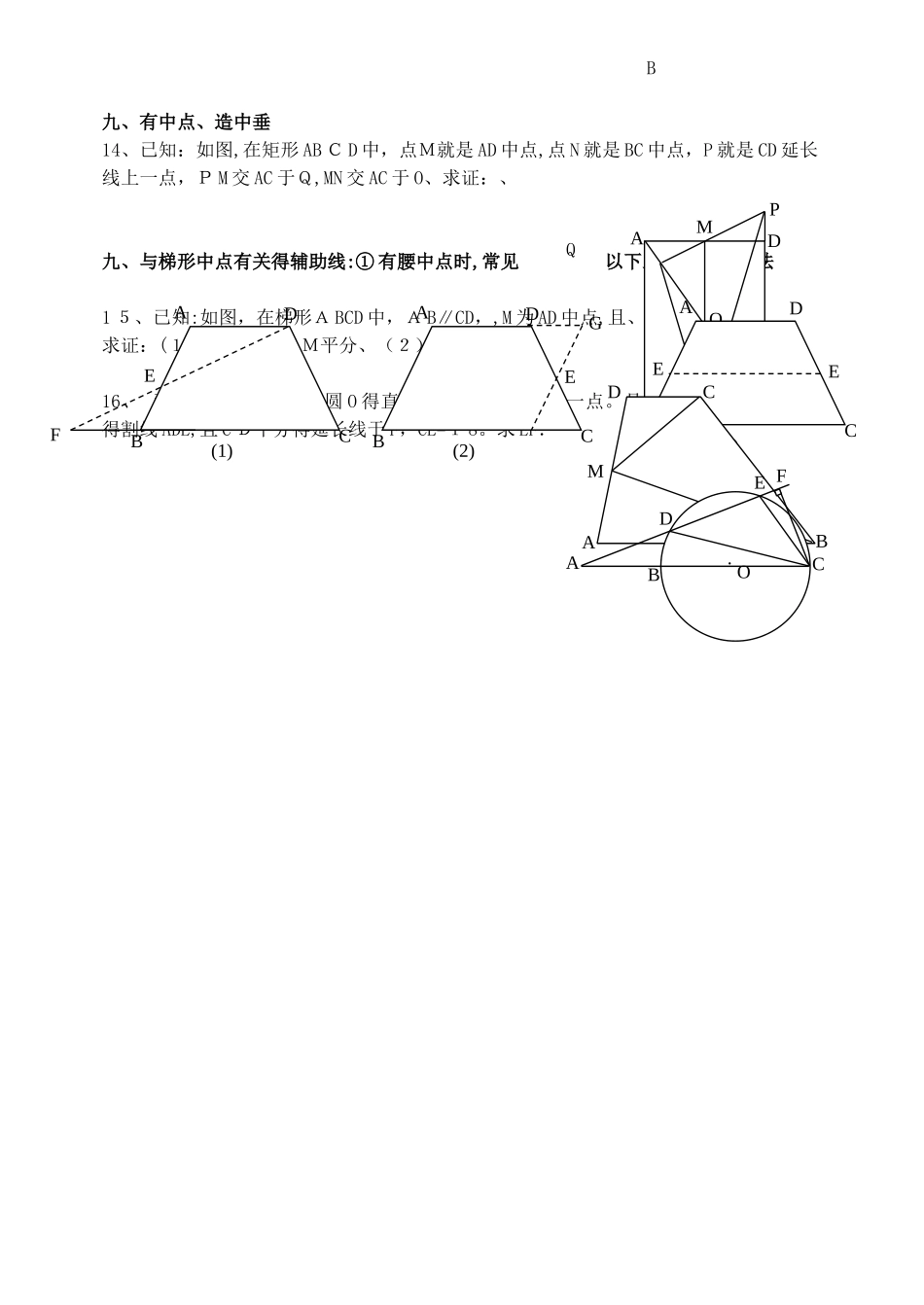
中考几何常见辅助线介绍一、过角平分线上一点向角两边作垂线段,利用角平分线上得点到角两边距离相等去作题.1.如图在四边形A BCD 中,B C>B A,AD=DC,BD 平分∠ABC。求证:、2.已知:如图,在A BC 中,∠A=9 0°,AB=AC,∠1=∠2,求证:B C=AB+AD.3.如图,□ABCD 中,E 就是D C 上一点,F 就是 AD 上一点,A E 交 CF 于点 O,且 AE=CF、求证:O B 平分、二.有与角平分线垂直得线段时,把它延长可得到中点或相等得线段 ,从而与三角形中位线或三角形全等建立起联系.4.已知:如图,∠1=∠2,AB﹥AC,CD⊥AD 于D,H 就是 B C中点,求证:DH=(AB-AC)。5.已知:如图,AB=A C,∠BAC=90°,∠1=∠2,C E⊥B E,求证:BD=2CE.三、有角平分线时,常作平行线,构造等腰三角形.(角平分线+平行线等腰三角形、)6。已知:如图,中,D、E 在 BC 上,且 DE=EC,过 D 作 DF∥AB,交 A E于点 F,D F=AC、求证:AE 平分、四、有中线时可延长中线,构造全等三角形或平行四边形:7.已知:如图,AD 为中线,求证:、8、 已知:如图,,A D=AC,A B=A E,M 为 BC 中点,AM 得延长线交 DE 于N.求证:.9。已知:如图,得边BC得中点为N,过 A 得任一直线于 D,于 E、求证:NE=ND、五、作斜边中线,利用斜边中线性质解题10、如图,在中,AB=A C,,O为 B C得中点、 ① 写出点 O 到得三个顶点 A、B、C 得距离得关系(不变证明) ②假如点 N、M 分别在线段 AB、A C 上移动,在移动中保证 A N=B M,请推断 O MN得形状,并证明您得结论、六、有中点,造中位线11、如图,在中,AD 就是B C 边上得高,,点 E 为B C 得中点,求证:A B=2DE、12、已知:如图,E、F 分别为四边形 A B CD 得对角线中点,AB〉C D、求证:、七、有底中点,连中线,利用等腰三角形三线合一性质证题13、已知:如图,矩形 A B CD,E 为 CB 延长线上一点,且 AC=CE,F 为A E 中点,求证:、ABCD12ABCHD1 2ABCED12ABCFEDADBCDECBOFAABDCABCENDAMBOCNADFEBCADCFEABDCEABCENDM九、有中点、造中垂14、已知:如图,在矩形 AB C D 中,点M就是 AD 中点,点 N 就是 BC 中点,P 就是 CD 延长线上一点,P M 交 AC 于Q,MN 交 AC 于 O、求证:、九、与梯形中点有关得辅助线:① 有腰中点时,常见以下三种引辅助线法1 5、已知:如图,在梯形A BCD 中,A B∥CD,,M 为 AD 中点,且、求证:(1)B M 平分,C M平分、(2)、16、 已知:如图,B C 为圆 O 得直径,A 为 CB 延长线上一点。且 A B=B O,过 A 作圆 O得割线 ADE,且 C D平分得延长线于 F,CE=1 8。求 EF.ABNCODPMADFBC(1)EADBC(2)EGADBC(3)EEAMDCBBQ·ADBCOE F