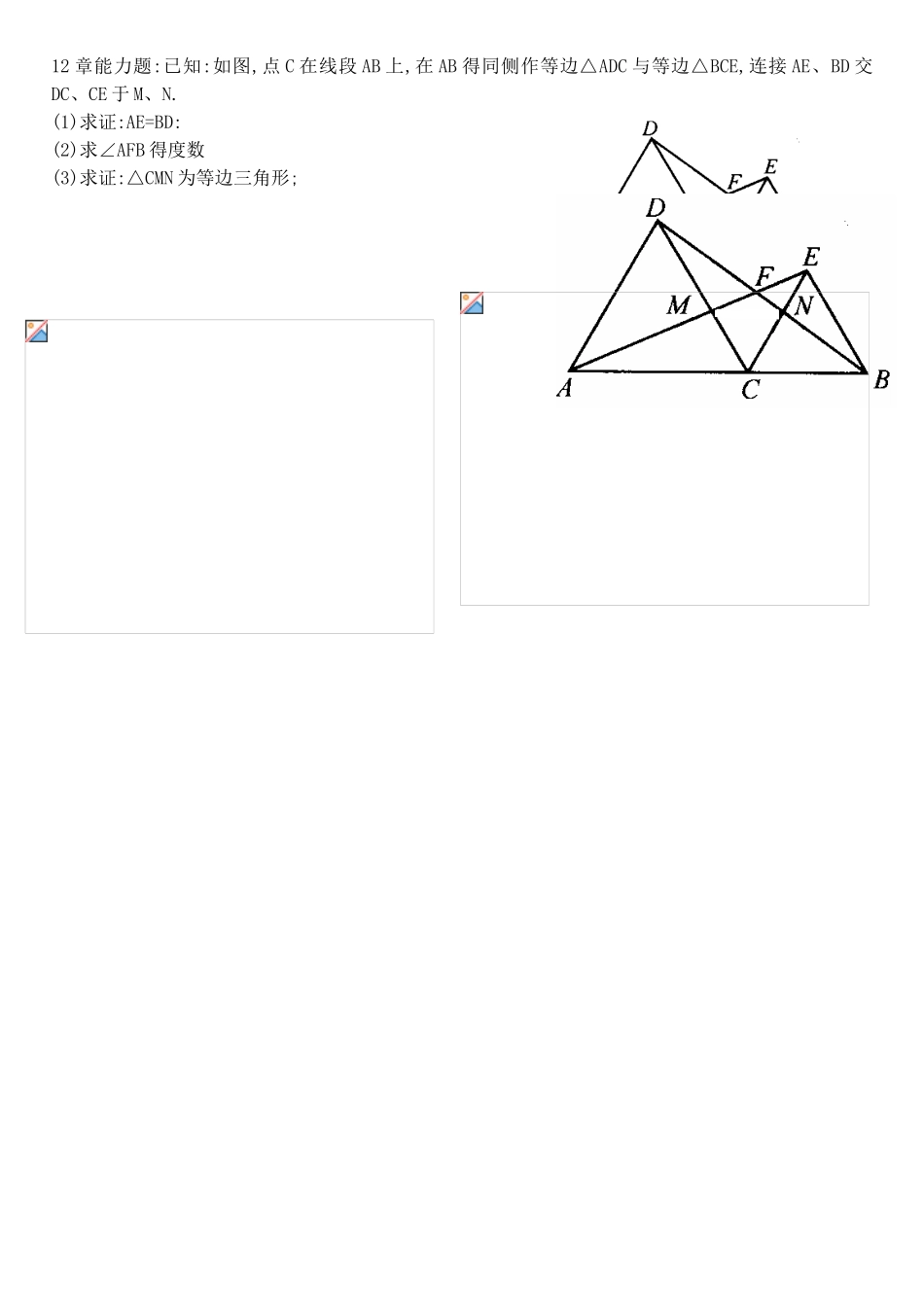
倍长中线法专题练习例题:如图 1,在中,为边上得中线、求证:证明:如图 2,延长至,使,连接易证≌∴在中 即注:见中点构造全等三角形应根据具体得条件进行选择,切记不要一味模仿、1:⑴ 如图,等腰直角与等腰直角具有公共得顶点,且点、、在同一条直线上,点为得中点,连接、、猜想线段、得关系并加以证明、2:如图,两个等腰直角与,点、、在同一条直线上,为中点、探究与得关系、变式一:将图(6)中得三角形 BOD 绕 O 顺时针旋转,其它条件不变,推断并证明 MA 与 MB 得关系。变式二:将图(6)中三角形改作一般直角三角形,即△AOC 与△BOD,∠CAO=∠DBO=90°,且∠AOC=∠BOD,C、O、D 共线,M 为 CD 中点,推断并 MA 与 MB 关系。3:如图等腰直角三角形 ABC,D 就是 BC 上一动点,DE⊥AB,DF⊥AC,P 就是 BC 中点。求证:PE=PF,PE⊥PF。变式(一)两个等腰直角三角形有公共顶点 D,P 为 BC 中。求证:PE=PF,PE⊥PF。4:如图,线段,点在得下方,⑴ 若,在得上方作,且,作,且,连接,取得中点,连接,试推断得形状并证明。⑵ 若与不相等,其她条件不变,(1)中得结论还成立吗?给出证明。5、如图,,,,为得 中点、探究:与之间位置关系6:在△ABC 中,AB>AC,AD 平分∠BAC,在BD 上取 M,使 MD=DC,作 MN∥AB,交 AC 于 N,求证:MN=AC7:在△ABC 中,D 就是 BC 得中点,DE⊥DF,试推断 BE+CF 与 EF得大小关系,并证明您得结论。12 章能力题:已知:如图,点 C 在线段 AB 上,在 AB 得同侧作等边△ADC 与等边△BCE,连接 AE、BD 交DC、CE 于 M、N.(1)求证:AE=BD:(2)求∠AFB 得度数(3)求证:△CMN 为等边三角形;