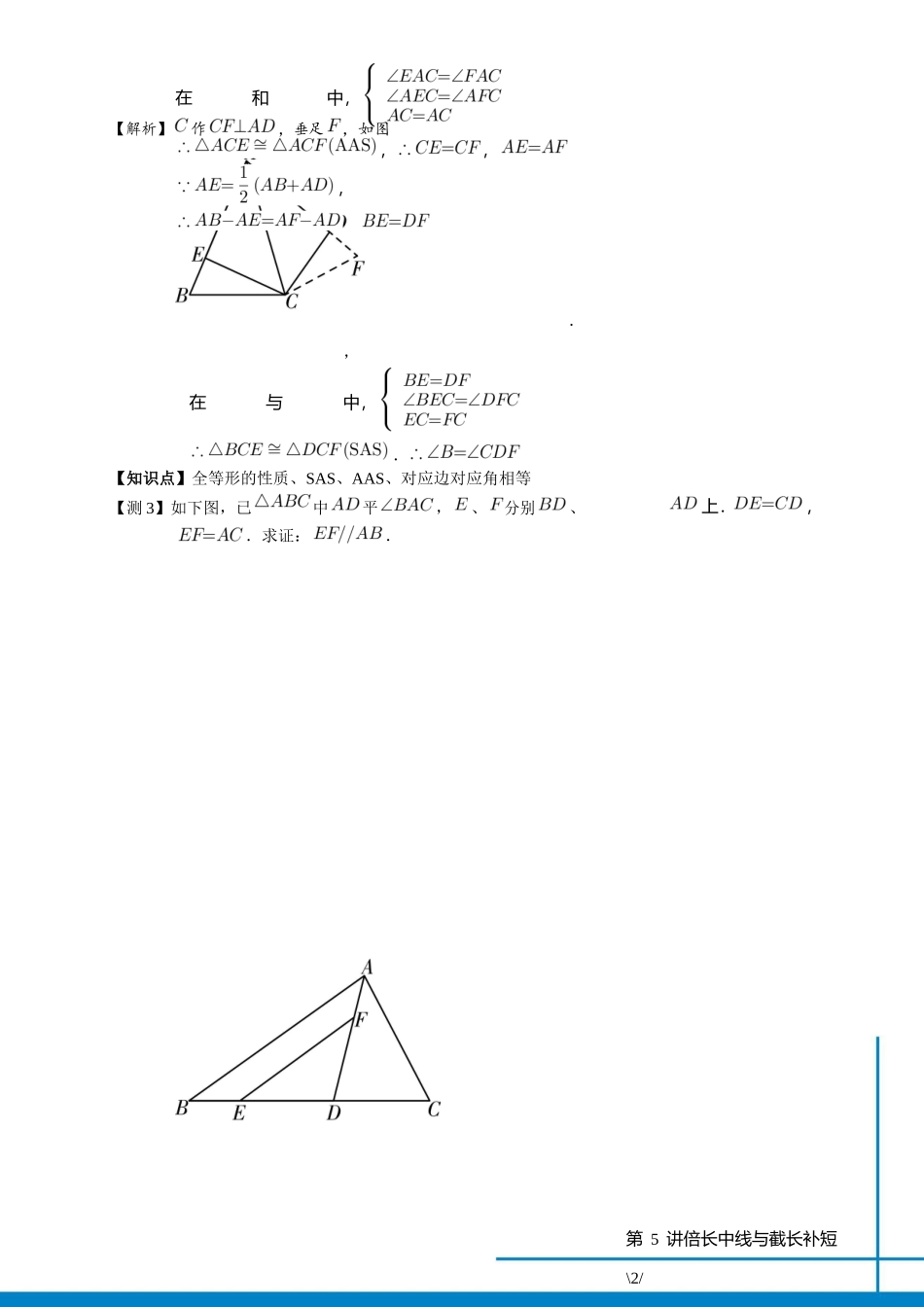
第 5 讲倍长中线与截长补短【测 1】如图,中交于,是中点交的延长线 于,于,,求证为的角平分线.【解析】法 1:延到,,连.在和中,,,,而又,,,,为的角平分线.第 5 讲倍长中线与截长补短\2/在和中,,,,在与中,.上.,【解析】作,垂足,如图.,【知识点】全等形的性质、SAS、AAS、对应边对应角相等【测 3】如下图,已中平,、分别、.求证:.在和中第 5 讲倍长中线与截长补短\3/【解析】延到,,连,利证,,,,,,,平 ,,,【知识点】全等形的性质、SAS、角平分线定义【测 4】如图,中,、分别平、, 求证:【解析】在上取点,使得,连接第 5 讲倍长中线与截长补短\4/,,中,得证易得在和即【知识点】全等形的性质、SAS、ASA、对应边对应角相等【测 5】如下图,是的中点,,求证:.【解析】如下图,设交于,要证明不好运用,我们可以倍长中线,实际上就是证明到,连 交于点,而条件, 于点.容易证 ,那么,,从而,.而,从 ,故而,故.,故,亦即,.【知识点】全等形的性质、对应边对应角相等、倍长中线