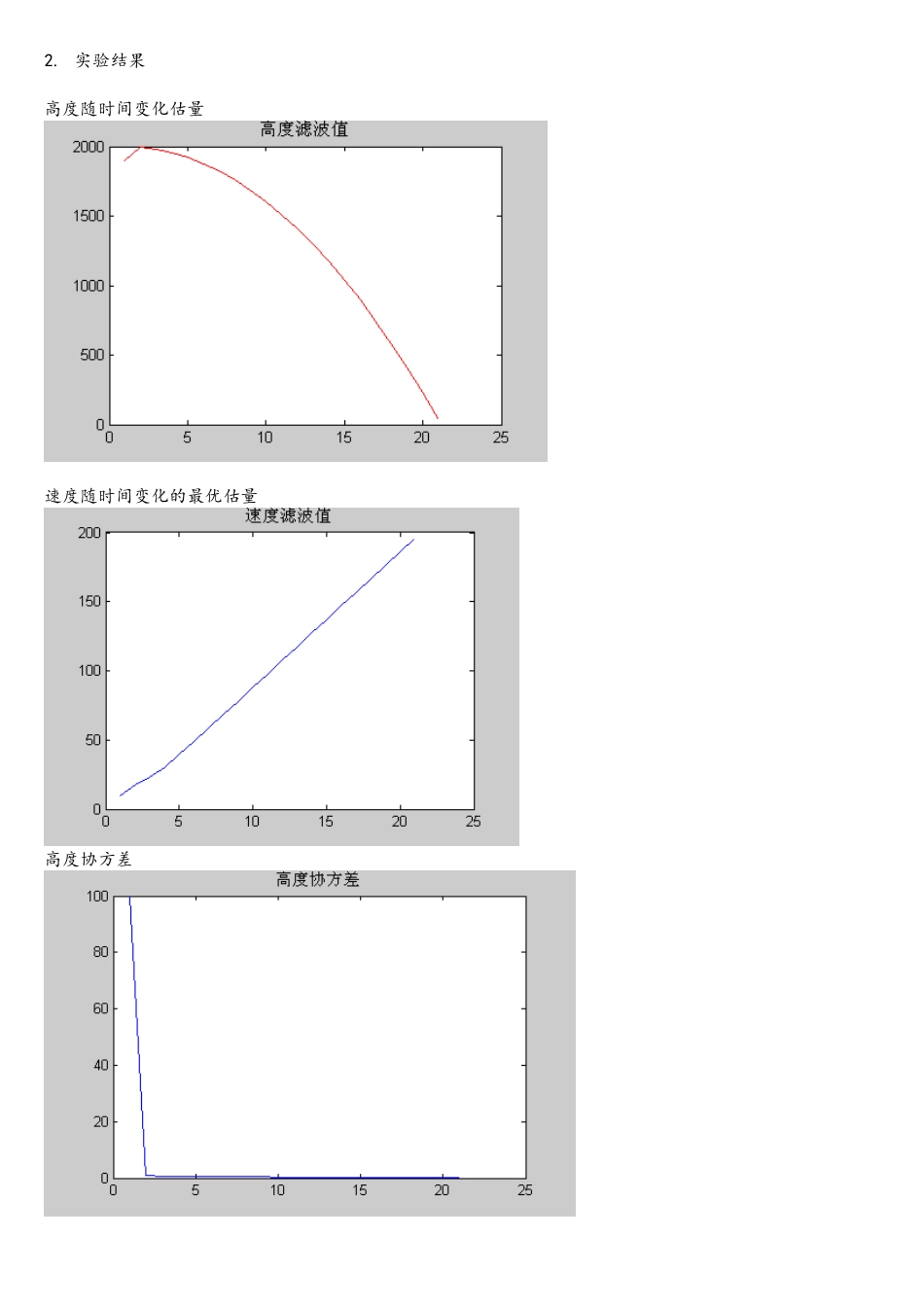
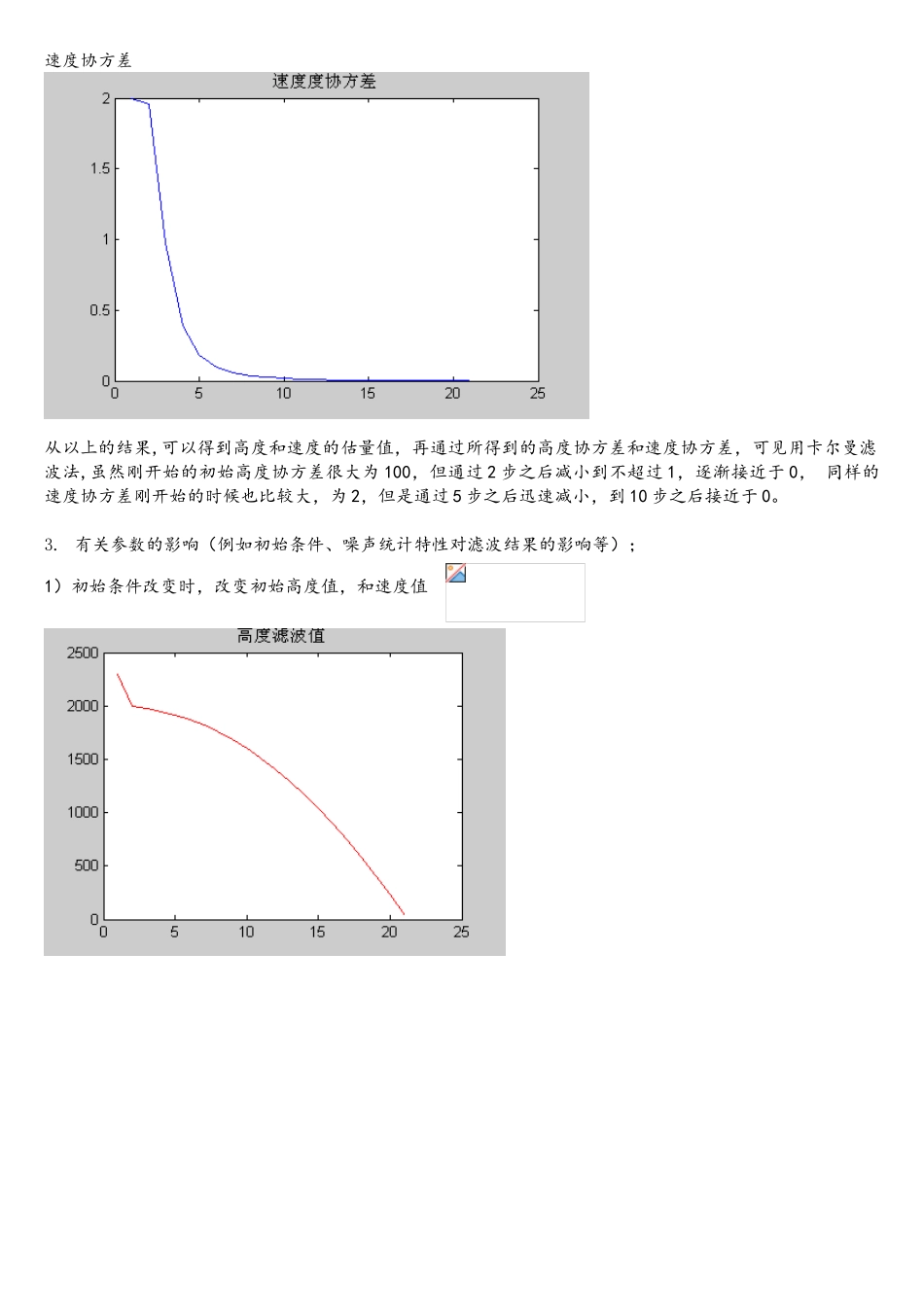
一。 已知一物体作自由落体运动,对其高度进行了 20 次测量,测量值如下表:时间[s]1234567高度[km]1.99451.97941.95541.92141。87771.82501.7598时间[s]891011121314高度[km]1。68671.60361。50921.40761.29441。17241.0399时间[s]151617181920高度[km]0.89800.74550.58500。41250。23180.0399设高度的测量误差是均值为 0、方差为 1 的高斯白噪声随机序列,该物体的初始高度和速度也是高斯分布的随机变量,且。试求该物体高度和速度随时间变化的最优估量。()解: 1。 令 t=1 R(k)=1 Q(k)=0 根据离散时间卡尔曼滤波公式,则有: = = =滤波初值: 一步预测: 滤波增益:滤波计算: 2. 实验结果高度随时间变化估量速度随时间变化的最优估量高度协方差速度协方差从以上的结果,可以得到高度和速度的估量值,再通过所得到的高度协方差和速度协方差,可见用卡尔曼滤波法,虽然刚开始的初始高度协方差很大为 100,但通过 2 步之后减小到不超过 1,逐渐接近于 0, 同样的速度协方差刚开始的时候也比较大,为 2,但是通过 5 步之后迅速减小,到 10 步之后接近于 0。3. 有关参数的影响(例如初始条件、噪声统计特性对滤波结果的影响等);1)初始条件改变时,改变初始高度值,和速度值 由实验结果分析可得度滤波值和速度滤波值在开始几步接近初始值,协方差值基本不变。2)当初始协方差值改变时,改为实验结果分析高度和速度滤波值基本不变,速度协方差和高度协方差开始要接近速度协方差和高度协方差的初始值。但是经过几步之后,都趋于 0.二.同样考虑自由落体运动的物体,用雷达(和物体落地点在同一水平面)进行测量,如图所示.假如,且雷达测距和测角的测量噪声是高斯白噪声随机序列,均值为零、方差阵,试根据下列测量数据确定物体的高度和速度随时间变化的估量值。时间[s]*1000斜距[km]俯仰角[rad]*1000 0.00050000000000 2.82741643781891 0.00075850435876 0.00100000000000 2。82519811729771 0.00083282260478 0。00150000000000 2.82066686966236 0。00067808241639 0。00200000000000 2。81487233105901 0.00085279036802 0.00250000000000 2.80671786536244 0。00072900768452 0。00300000000000 2。79725268974089 0.00080072481819 0。00350000000000 2。78664273475039 0。00075095576213 0。00400000000000 2.77320365026313 0。00065762725379 0。00450000000000...