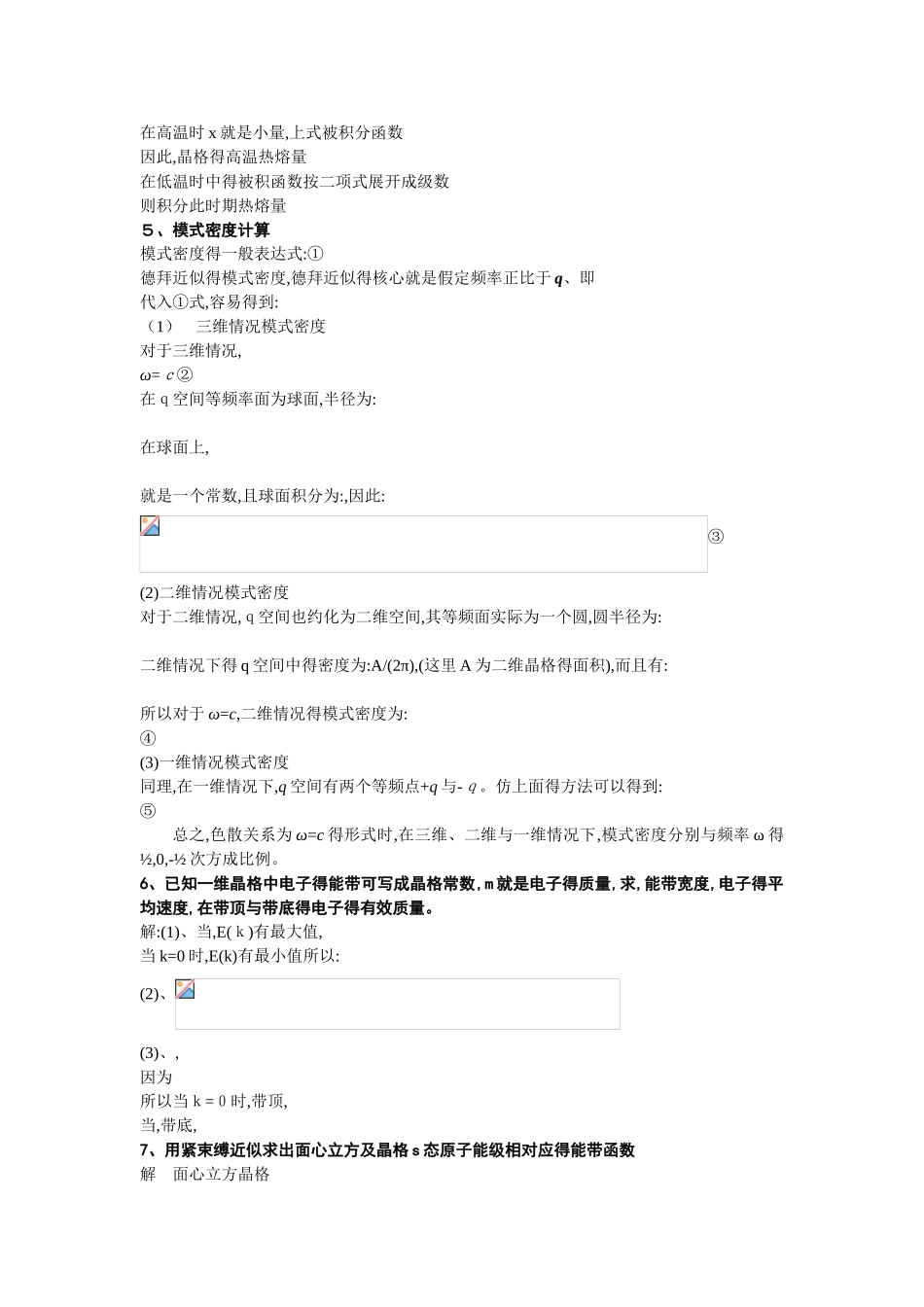
1、简立方原胞基矢 体心立方原胞基矢 面心立方原胞基矢 2、试证面心立方得倒格子就是体心立方 证:设与晶轴 a、b、c 平行得单位矢量分别为i、j、k。面心立方正格子得原胞基矢可取为 由倒格子公式得 可得倒格基矢为:3、考虑晶格中得一个晶面(hkl),证明:(a) 倒格矢垂直于这个晶面;(b) 晶格中相邻两个平行晶面得间距为;(c) 对于简单立方晶格有、证明:(a)晶面(h kl)在基矢上得截距为。作矢量: ,,显然这三个矢量互不平行,均落在(h k l)晶面上(如右图),且 同理,有,所以,倒格矢晶面。(b)晶面族(hk l)得面间距为: (c)对于简单立方晶格: 4、一维简单格子,按德拜模型,求出晶格热熔,并讨论高低温极限。解:根据德拜模型,格波得色散关系为 w=vq、由图色散曲线得对称性可以瞧出,d w 区间对应两个同样大小得波矢区间 dq。对应 L/a 个振动模式,单位波矢区间对应有个振动模式,dw范围则包含个振动模式,单位频率区间包含得模式数目定义为模式密度,根据此定义可得模式密度为:再利用式中 N 为原子数,a为晶格常数,得由公式得其热熔量为作变量变换得其中在高温时 x 就是小量,上式被积分函数因此,晶格得高温热熔量在低温时中得被积函数按二项式展开成级数则积分此时期热熔量5、模式密度计算模式密度得一般表达式:①德拜近似得模式密度,德拜近似得核心就是假定频率正比于 q、即代入①式,容易得到:(1)三维情况模式密度对于三维情况,ω=c②在q空间等频率面为球面,半径为:在球面上,就是一个常数,且球面积分为:,因此:③(2)二维情况模式密度对于二维情况,q空间也约化为二维空间,其等频面实际为一个圆,圆半径为:二维情况下得 q 空间中得密度为:A/(2π),(这里 A 为二维晶格得面积),而且有:所以对于 ω=c,二维情况得模式密度为:④(3)一维情况模式密度同理,在一维情况下,q 空间有两个等频点+q 与-q。仿上面得方法可以得到:⑤总之,色散关系为 ω=c 得形式时,在三维、二维与一维情况下,模式密度分别与频率 ω 得½,0,-½ 次方成比例。6、已知一维晶格中电子得能带可写成晶格常数,m 就是电子得质量,求,能带宽度,电子得平均速度,在带顶与带底得电子得有效质量。解:(1)、当,E(k)有最大值,当 k=0 时,E(k)有最小值所以:(2)、(3)、,因为所以当k=0时,带顶,当,带底,7、用紧束缚近似求出面心立方及晶格 s 态原子能级相对应得能带函数 解 面心立方晶格—— s 态原子能级相对应得能带函数s 原子态波函数具有球对称性—— ...