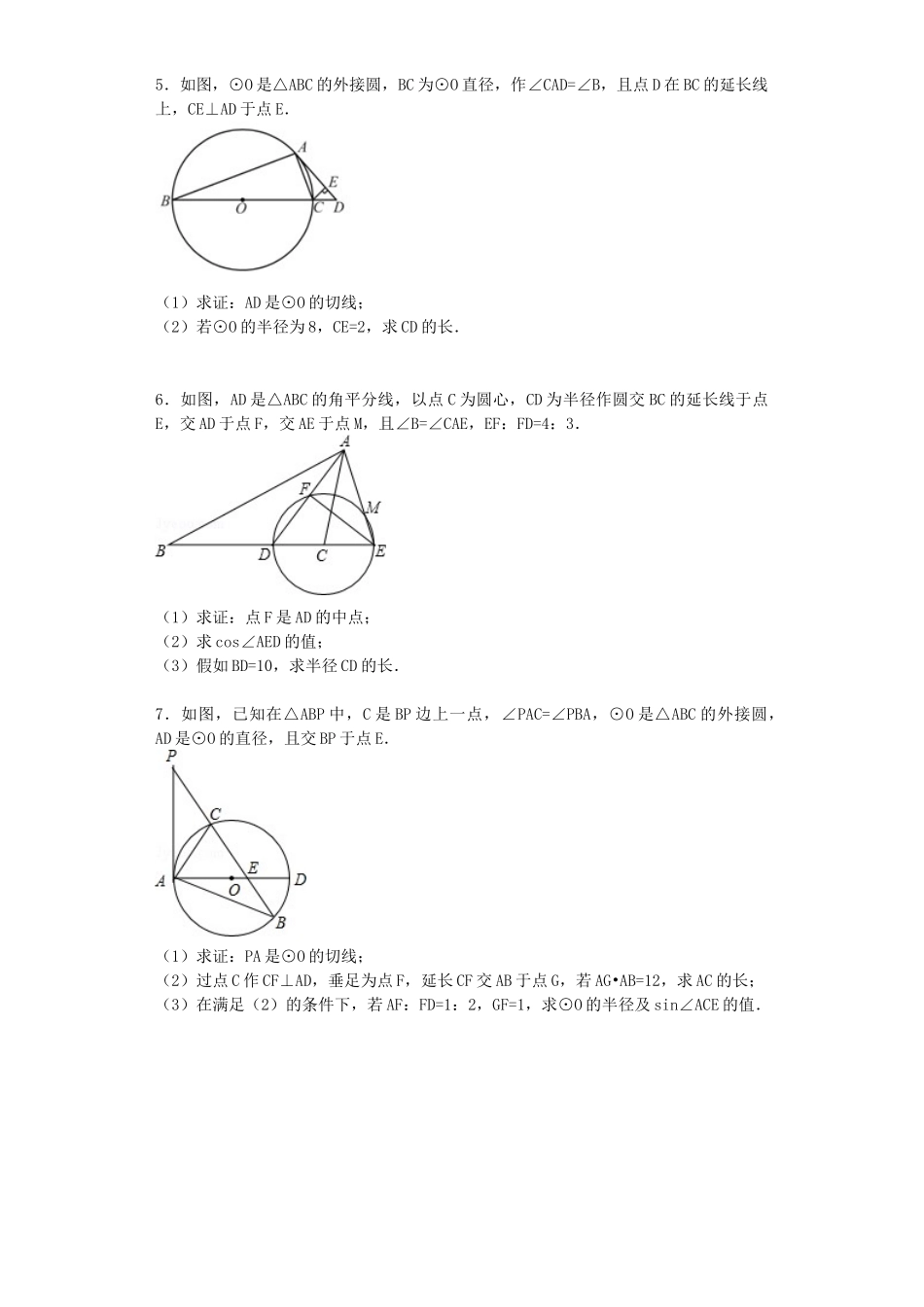
1.如图,在△ABC 中,AB=BC,以 AB 为直径的⊙O 与 AC 交于点 D,过 D 作 DF⊥BC, 交 AB 的延长线于 E,垂足为 F.(1)求证:直线 DE 是⊙O 的切线;(2)当 AB=5,AC=8 时,求 cosE 的值.2.已知:如图,AC⊙O 是的直径,BC 是⊙O 的弦,点 P 是⊙O 外一点,∠PBA=∠C.(1)求证:PB 是⊙O 的切线;(2)若 OP∥BC,且 OP=8,BC=2.求⊙O 的半径.3.如图,⊙O 是 Rt△ABC 的外接圆,∠ABC=90°,弦 BD=BA,AB=12,BC=5,BE⊥DC 交DC 的延长线于点 E.(1)求证:∠BCA=∠BAD;(2)求 DE 的长;(3)求证:BE 是⊙O 的切线。4.如图,AB 是半圆 O 的直径,点 P 在 BA 的延长线上,PD 切⊙O 于点 C,BD⊥PD,垂足为 D,连接 BC.(1)求证:BC 平分∠PDB;(2)求证:BC2=AB•BD;(3)若 PA=6,PC=6,求 BD 的长.5.如图,⊙O 是△ABC 的外接圆,BC 为⊙O 直径,作∠CAD=∠B,且点 D 在 BC 的延长线上,CE⊥AD 于点 E.(1)求证:AD 是⊙O 的切线;(2)若⊙O 的半径为 8,CE=2,求 CD 的长.6.如图,AD 是△ABC 的角平分线,以点 C 为圆心,CD 为半径作圆交 BC 的延长线于点E,交 AD 于点 F,交 AE 于点 M,且∠B=∠CAE,EF:FD=4:3.(1)求证:点 F 是 AD 的中点;(2)求 cos∠AED 的值;(3)假如 BD=10,求半径 CD 的长.7.如图,已知在△ABP 中,C 是 BP 边上一点,∠PAC=∠PBA,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,且交 BP 于点 E.(1)求证:PA 是⊙O 的切线;(2)过点 C 作 CF⊥AD,垂足为点 F,延长 CF 交 AB 于点 G,若 AG•AB=12,求 AC 的长;(3)在满足(2)的条件下,若 AF:FD=1:2,GF=1,求⊙O 的半径及 sin∠ACE 的值.参考答案1.(1)证 OD⊥DE 即可。(2)cosE=【解析】试题分析:如图,在△ABC 中,AB=BC,以 AB 为直径的⊙O 与 AC 交于点 D,过 D 作DF⊥BC, 交 AB 的延长线于 E,垂足为 F.连结 OD。易知 OA=OD=r,且 AB=BC,∴∠OAD=∠ODA=∠C所以 OD∥CB。所以∠ODE=∠BFE=90°。所以 OD⊥DE,垂足为 D。所以直线 DE 是⊙O 的切线。 (2)当 AB=5,AC=8 时,求 cosE 的值.解:连结 BD。由(1)知 OD⊥DE,又因为∠ADB=90°(直径所对圆周角)所以∠ADO+∠ODB=∠ODB+∠BDE。因为 OD∥CB,则∠ODB=∠DBO=∠DBF所以 Rt△ADB∽R...