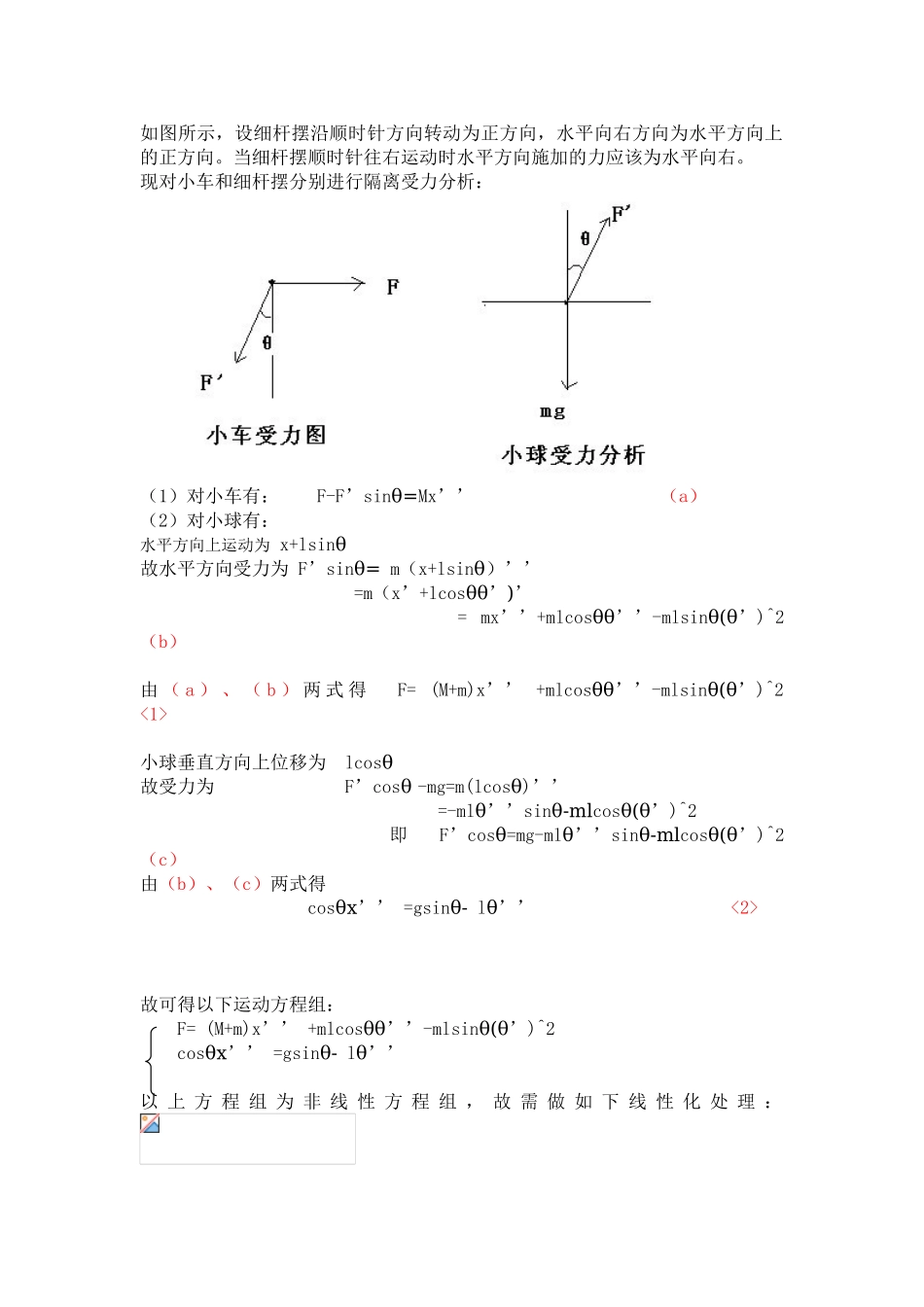
深圳大学考试答题纸(以论文、报告等形式考核专用)二○○ 九 ~二○○ 一零 学年度第 2 学期课程编号课程名称计算机控制系统 主讲老师李东评分学 号姓名专业年级2025 级光电工程学院测控技术与仪器老师评语:题目:一级倒立摆模型的仿真一、倒立摆模型的讨论意义倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。对倒立摆系统的讨论能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等。故其讨论意义广泛。二、倒立摆模型的数学建模质量为 m 的小球固结于长度为 L 的细杆(可忽略杆的质量)上,细杆又和质量为 M 的小车铰接相连。由经验知:通过控制施加在小车上的力 F(包括大小和方向)能够使细杆处于 θ=0 的稳定倒立状态。在忽略其他零件的质量以及各种摩擦和阻尼的条件下,推导小车倒立摆系统的数学模型 分析过程如下: 如图所示,设细杆摆沿顺时针方向转动为正方向,水平向右方向为水平方向上的正方向。当细杆摆顺时针往右运动时水平方向施加的力应该为水平向右。 现对小车和细杆摆分别进行隔离受力分析: (1)对小车有: F-F’sinθ=Mx’’ (a)(2)对小球有: 水平方向上运动为 x+lsinθ故水平方向受力为 F’sinθ= m(x+lsinθ)’’ =m(x’+lcosθθ’)’ = mx’’+mlcosθθ’’-mlsinθ(θ’)^2 (b) 由 ( a ) 、 ( b ) 两 式 得 F= (M+m)x’’ +mlcosθθ’’-mlsinθ(θ’)^2 <1>小球垂直方向上位移为 lcosθ故受力为 F’cosθ -mg=m(lcosθ)’’ =-mlθ’’sinθ-mlcosθ(θ’)^2 即 F’cosθ=mg-mlθ’’sinθ-mlcosθ(θ’)^2 (c)由(b)、(c)两式得 cosθx’’ =gsinθ- lθ’’ <2> 故可得以下运动方程组: F= (M+m)x’’ +mlcosθθ’’-mlsinθ(θ’)^2 cosθx’’ =gsinθ- lθ’’以 上 方 程 组 为 非 线 性 方 程 组 , 故 需 做 如 下 线 性 化 处 理 :当 θ 很小时,由 cosθ、sinθ 的幂级数展开式可知,忽略高次项后,可得 cosθ≈1,sinθ≈...