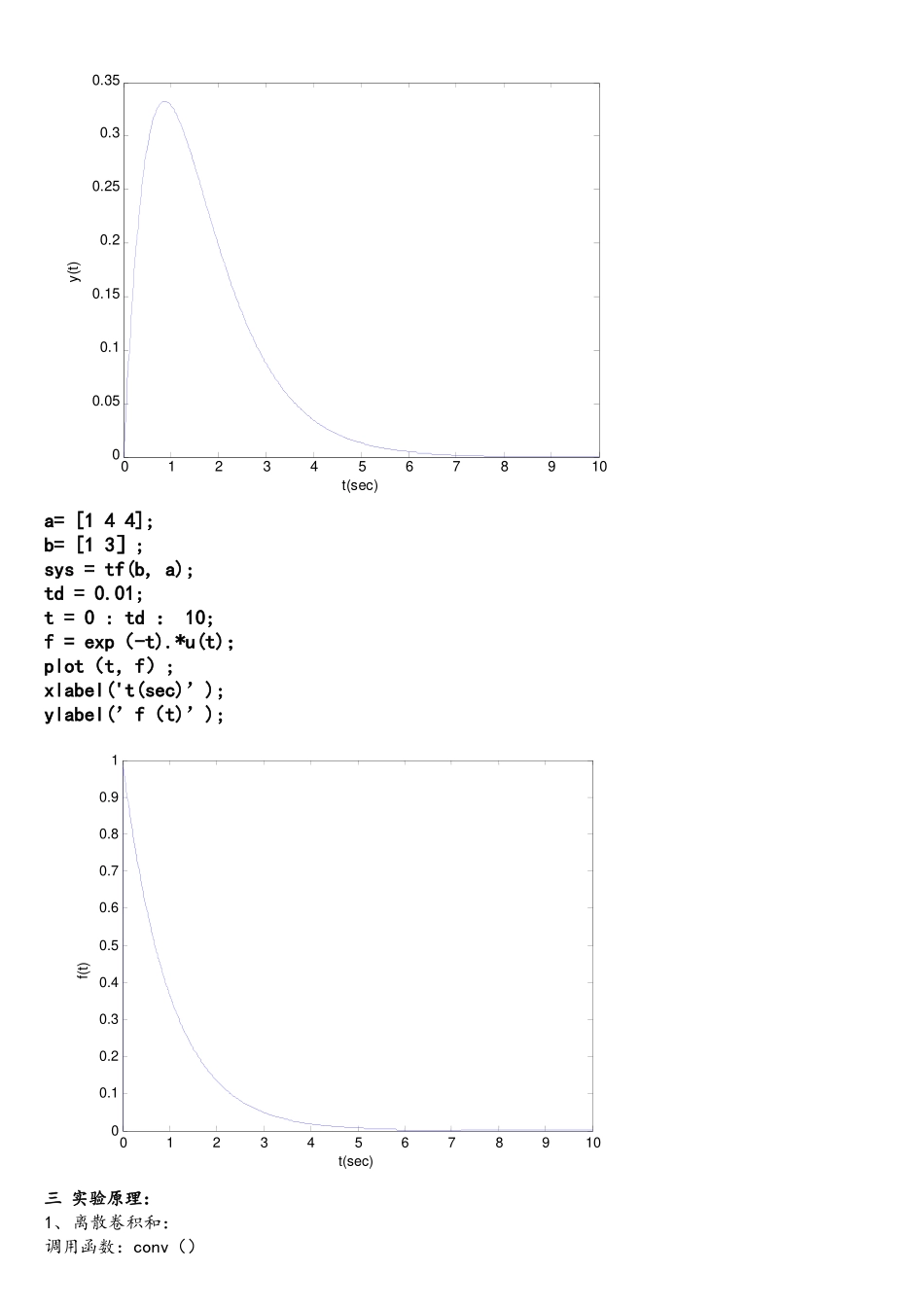
实验五 使用 matlab 实现卷积的运算一 实验目的1、学习 MATLAB 语言的编程方法及熟悉 MATLAB 指令;2、深刻理解卷积运算,利用离散卷积实现连续卷积运算;二 实验内容1、 完成与两函数的卷积运算其中:在一个图形窗口中,画出、以及卷积结果.要求每个坐标系有标题、坐标轴名称。>〉 p=0。1;t=0:p:10;f1=exp(-2*t).*u(t); f2=u(t)—u(t—4);f=conv(f1,f2);subplot(1,3,1);plot(t,f1,’r');title(’f1(t)=e^—2*t*u(t)’);xlabel(’t(sec)’);ylabel(’f1(t)’);subplot(1,3,2);plot(t,f2,'g');title(’f2(t)=u(t)-u(t—4)');xlabel('t(sec)’);ylabel('f2(t)’);subplot(1,3,3);plot(f);title('f(t)=f1(t)*f2(t)’);xlabel('t(sec)');ylabel('f(t)’);051000.10.20.30.40.50.60.70.80.9f1(t)=e-2*t*u(t)t(sec)f1(t)051000.10.20.30.40.50.60.70.80.91f2(t)=u(t)-u(t-4)t(sec)f2(t)020040000.511.522.533.544.55f(t)=f1(t)*f2(t)t(sec)f(t)2、若系统模型为: 其中 求零状态响应,画出波形(函数本身画出一幅图,自己再画出一幅输入波形图)。a=[1 4 4];b=[1 3];sys=tf(b,a);td=0.01;t=0:td:10;f=exp(—t).*u(t);y=lsim(sys,f,t);plot(t,y);xlabel('t(sec)');ylabel('y(t)');01234567891000.050.10.150.20.250.30.35t(sec)y(t)a= [1 4 4]; b= [1 3]; sys = tf(b, a); td = 0.01; t = 0 : td : 10; f = exp(-t).*u(t);plot(t,f);xlabel('t(sec)’); ylabel(’f(t)’);三 实验原理:1、离散卷积和:调用函数:conv()01234567891000.10.20.30.40.50.60.70.80.91t(sec)f(t)为离散卷积和,其中,f1(k), f2 (k) 为离散序列,K=…-2, -1, 0 , 1, 2, …。但是,conv 函数只给出纵轴的序列值的大小,而不能给出卷积的 X 轴序号。为得到该值,进行以下分析:对任意输入:设非零区间 n1~n2,长度 L1=n2—n1+1;非零区间 m1~m2,长度 L2=m2—m1+1.则:非零区间从 n1+m1 开始,长度为 L=L1+L2-1,所以 S(K)的非零区间为:n1+m1~ n1+m1+L—1.2、连续卷积和离散卷积的关系:计算机本身不能直接处理连续信号,只能由离散信号进行近似:设一系统(LTI)输入为,输出为,如图所示。 t 若输入为 f(t):得输出:当时:所以:假如只求离散点上的 f 值LTI所以,可以用离散卷积和 CONV()求连续卷积,只需足够小以及在卷积和的基础上乘以。3、连续卷积坐标的确定:设非零值坐标范围:t1~t2,间隔 P 非零值坐标范围:tt1~tt2,间隔 P非零值坐标:t1+tt1~t2+tt2