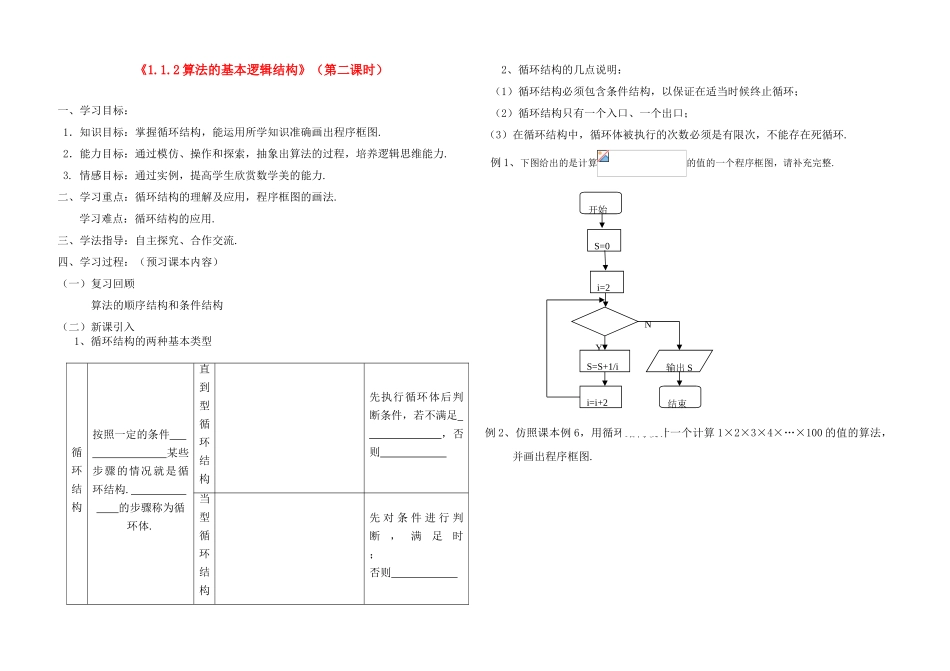
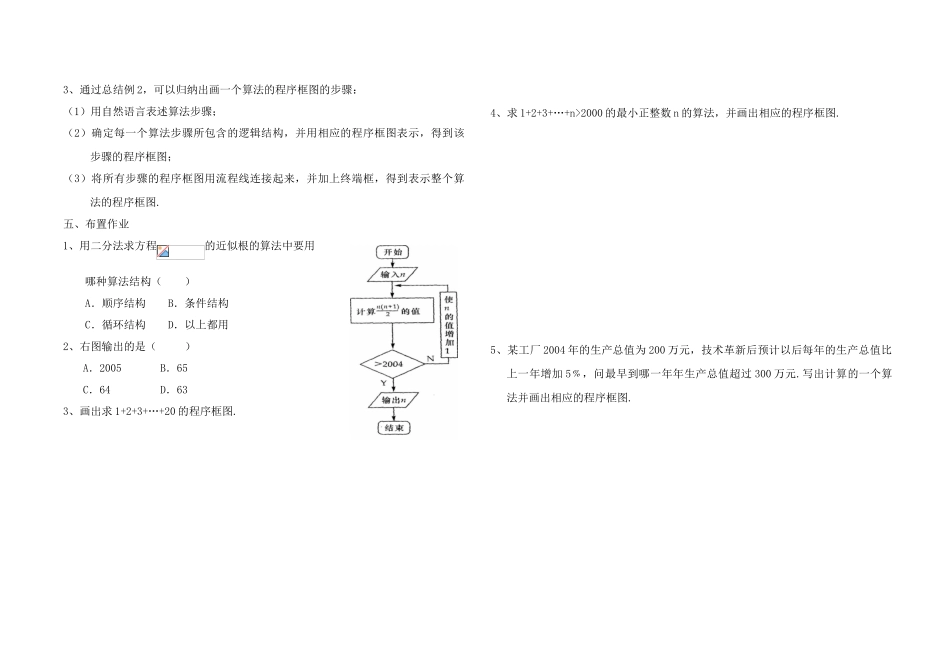
《1.1.2 算法的基本逻辑结构》(第二课时)一、学习目标:1.知识目标:掌握循环结构,能运用所学知识准确画出程序框图.2.能力目标:通过模仿、操作和探索,抽象出算法的过程,培养逻辑思维能力.3. 情感目标:通过实例,提高学生欣赏数学美的能力.二、学习重点:循环结构的理解及应用,程序框图的画法.学习难点:循环结构的应用.三、学法指导:自主探究、合作交流.四、学习过程:(预习课本内容)(一)复习回顾 算法的顺序结构和条件结构(二)新课引入1、循环结构的两种基本类型 2、循环结构的几点说明: (1)循环结构必须包含条件结构,以保证在适当时候终止循环; (2)循环结构只有一个入口、一个出口;(3)在循环结构中,循环体被执行的次数必须是有限次,不能存在死循环.例 1、下图给出的是计算的值的一个程序框图,请补充完整.例 2、仿照课本例 6,用循环结构设计一个计算 1×2×3×4×…×100 的值的算法,并画出程序框图.循环结构按照一定的条件 某些步骤的情况就是循环结构. 的步骤称为循环体.直到型循环结构先执行循环体后判断条件,若不满足 ,否则 当型循环结构先 对 条 件 进 行 判断,满足时 ;否则 Y开始S=0i=2S=S+1/ii=i+2N输出 S结束3、通过总结例 2,可以归纳出画一个算法的程序框图的步骤:(1)用自然语言表述算法步骤;(2)确定每一个算法步骤所包含的逻辑结构,并用相应的程序框图表示,得到该步骤的程序框图;(3)将所有步骤的程序框图用流程线连接起来,并加上终端框,得到表示整个算法的程序框图.五、布置作业1、用二分法求方程的近似根的算法中要用哪种算法结构( )A.顺序结构 B.条件结构 C.循环结构 D.以上都用2、右图输出的是( )A.2005 B.65 C.64 D.633、画出求 1+2+3+…+20 的程序框图. 4、求 1+2+3+…+n>2000 的最小正整数 n 的算法,并画出相应的程序框图.5、某工厂 2004 年的生产总值为 200 万元,技术革新后预计以后每年的生产总值比上一年增加 5﹪,问最早到哪一年年生产总值超过 300 万元.写出计算的一个算法并画出相应的程序框图.六、课后反思: