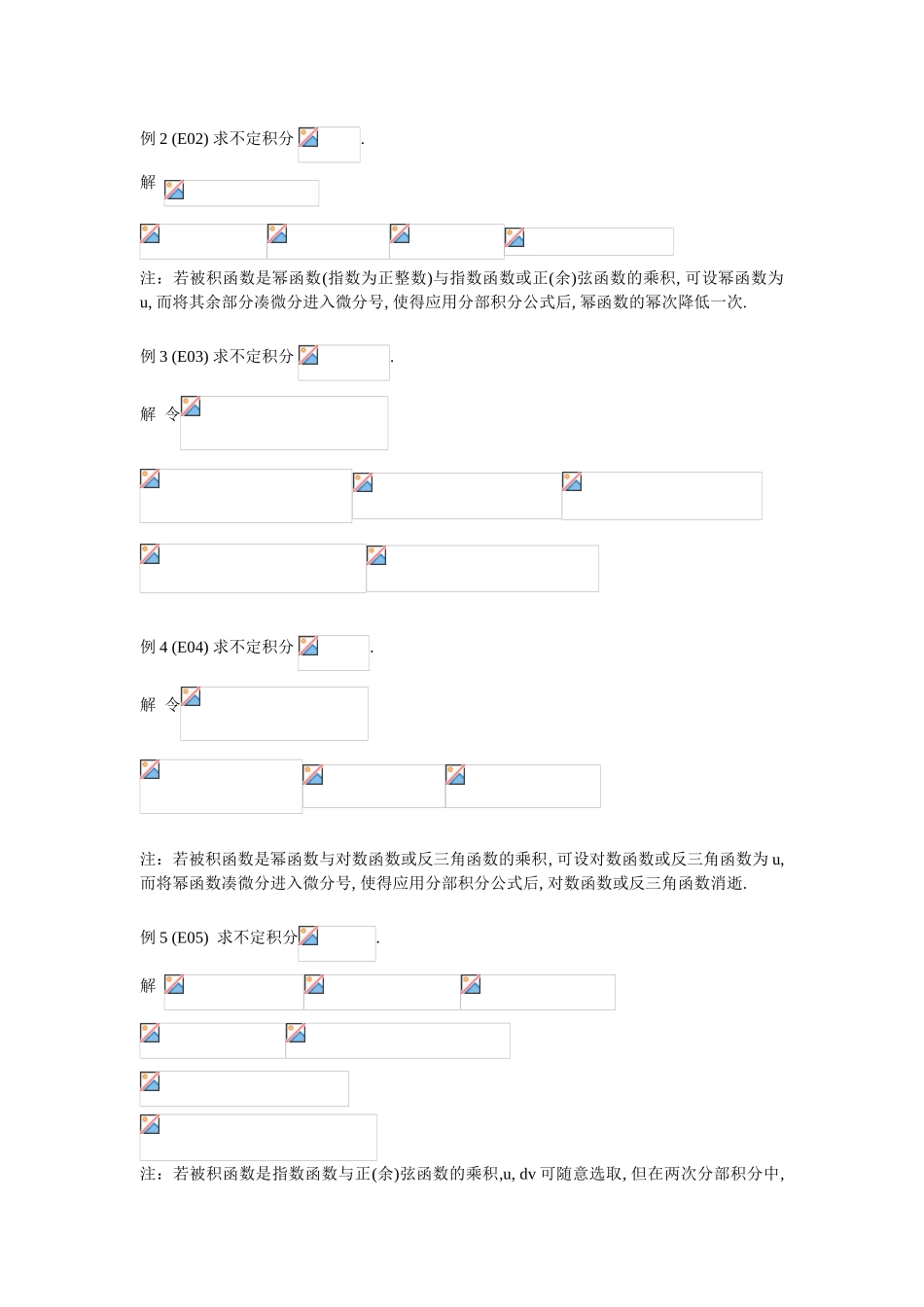
第三节 分部积分法分布图示★ 分部积分公式 ★ 几点说明★ 例 1 ★ 例 2 ★ 例 3 ★ 例 4★ 例 5 ★ 例 6 ★ 例 7 ★ 例 8★ 例 9 ★ 例 10 ★ 例 11 ★ 例 12★ 例 13 ★ 例 14 ★ 例 15 ★ 例 16★ 例 17 ★ 例 18★ 分部积分的列表法★ 例 19 ★ 例 20 ★ 例 21 ★ 例 22★ 内容小结 ★ 课堂练习★ 习题 4-3内容要点 分部积分公式: (3.1) (3.2)分部积分法实质上就是求两函数乘积的导数(或微分)的逆运算. 一般地, 下列类型的被积函数常考虑应用分部积分法(其中 m, n 都是正整数).例题选讲例 1 (E01) 求不定积分 .解一 令显然, 选择不当,积分更难进行.解二 令例 2 (E02) 求不定积分 .解 注:若被积函数是幂函数(指数为正整数)与指数函数或正(余)弦函数的乘积, 可设幂函数为u, 而将其余部分凑微分进入微分号, 使得应用分部积分公式后, 幂函数的幂次降低一次.例 3 (E03) 求不定积分 .解 令例 4 (E04) 求不定积分 .解 令注:若被积函数是幂函数与对数函数或反三角函数的乘积, 可设对数函数或反三角函数为 u, 而将幂函数凑微分进入微分号, 使得应用分部积分公式后, 对数函数或反三角函数消逝.例 5 (E05) 求不定积分.解 注:若被积函数是指数函数与正(余)弦函数的乘积,u, dv 可随意选取, 但在两次分部积分中, 必须选用同类型的 u, 以便经过两次分部积分后产生循环式, 从而解出所求积分.例 6 (E06) 求不定积分.解 灵活应用分部积分法,可以解决许多不定积分的计算问题. 下面再举一些例子,请读者悉心体会其解题方法.例 7 (E07) 求不定积分 .解 由于上式右端的第三项就是所求的积分把它移到等号左端去,再两端各除以 2,便得例 8 求不定积分解 例 9 求不定积分解 原式例 10 (E08) 求不定积分.解 令则于是例 11 求不定积分.解 令则例 12 求解法 1 先分部积分,后换元.设则于是 再设则于是代入上式, 得解法 2 先换元, 后分部积分.设则再设则例 13 求不定积分解 令则于是原式其中例 14 (E09) 求不定积分, 其中 n 为正整数.解 用分部积分法,当时有即 于是 以此作递推公式,并由即可得例 15 (E10) 已知的一个原函数是, 求.解 根据题意再注意到 两边同时对求导,得例 16 求不定积分解 先折成两个不定积分,再利用分部积分法.原式例 17 求不定积分解 例 18 求不定积分....