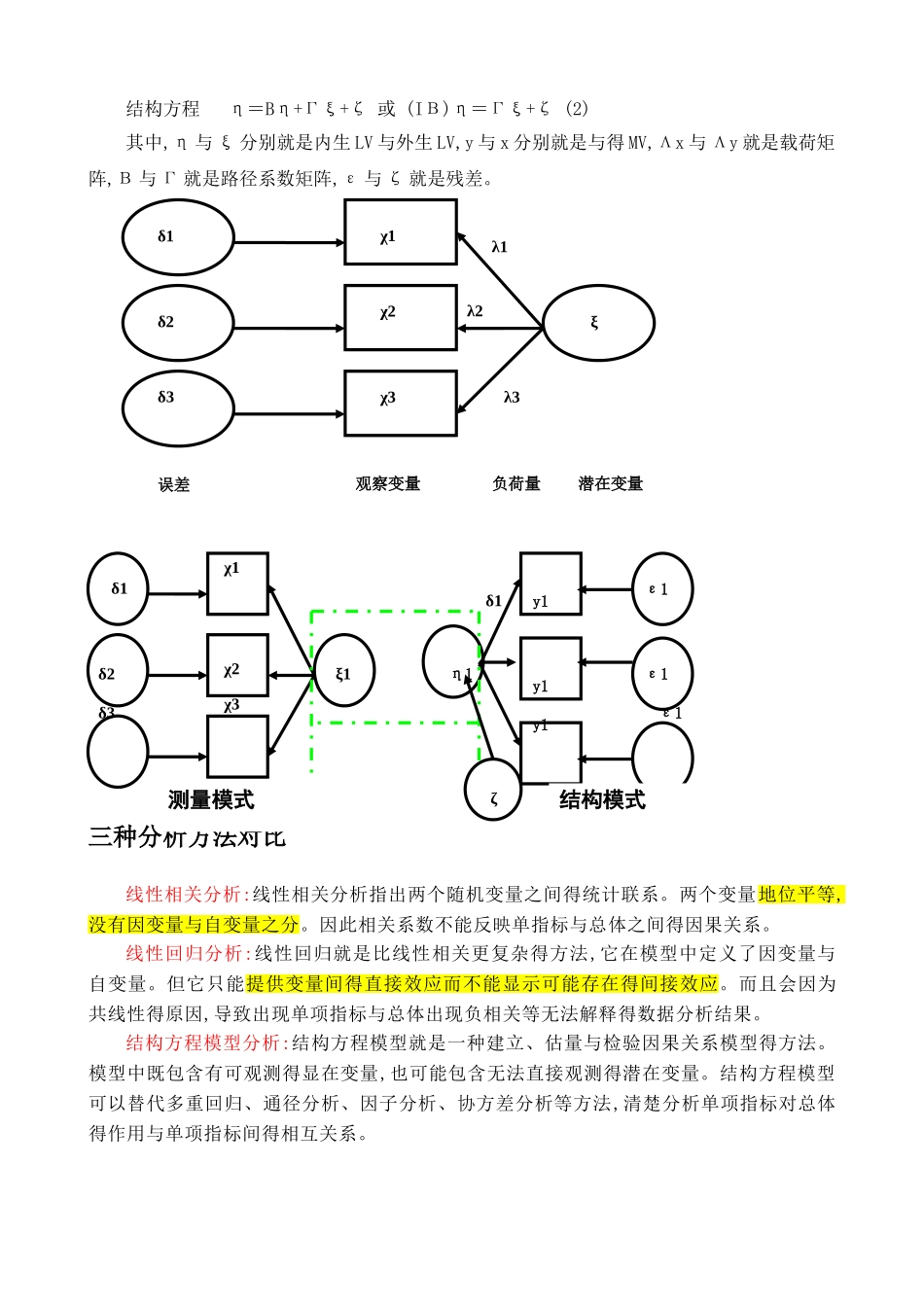
结构方程模型(Structural Equation Modeling,SEM) 20 世纪——主流统计方法技术:因素分析 回归分析20 世纪 70 年代:结构方程模型时代正式来临结构方程模型就是一门基于统计分析技术得讨论方法学 ,它主要用于解决社会科学讨论中得多变量问题,用来处理复杂得多变量讨论数据得探究与分析。在社会科学及经济、市场、管理等讨论领域,有时需处理多个原因、多个结果得关系,或者会碰到不可直接观测得变量(即潜变量),这些都就是传统得统计方法不能很好解决得问题。SEM 能够对抽象得概念进行估量与检定,而且能够同时进行潜在变量得估量与复杂自变量/因变量预测模型得参数估量。结构方程模型就是一种非常通用得、主要得线形统计建模技术,广泛应用于心理学、经济学、社会学、行为科学等领域得讨论。实际上,它就是计量经济学、计量社会学与计量心理学等领域得统计分析方法得综合。多元回归、因子分析与通径分析等方法都只就是结构方程模型中得一种特例。结构方程模型就是利用联立方程组求解,它没有很严格得假定限制条件,同时允许自变量与因变量存在测量误差。在许多科学领域得讨论中,有些变量并不能直接测量。实际上,这些变量基本上就是人们为了理解与讨论某类目得而建立得假设概念,对于它们并不存在直接测量得操作方法。人们可以找到一些可观察得变量作为这些潜在变量得“标识”,然而这些潜在变量得观察标识总就是包含了大量得测量误差。在统计分析中,即使就是对那些可以测量得变量,也总就是不断受到测量误差问题得侵扰。自变量测量误差得发生会导致常规回归模型参数估量产生偏差。虽然传统得因子分析允许对潜在变量设立多元标识,也可处理测量误差,但就是,它不能分析因子之间得关系。只有结构方程模型即能够使讨论人员在分析中处理测量误差,又可分析潜在变量之间得结构关系。简单而言,与传统得回归分析不同,结构方程分析能同时处理多个因变量,并可比较及评价不同得理论模型。与传统得探究性因子分析不同,在结构方程模型中,我们可以提出一个特定得因子结构,并检验它就是否吻合数据。通过结构方程多组分析,我们可以了解不同组别内各变量得关系就是否保持不变,各因子得均值就是否有显著差异。” 目前,已经有多种软件可以处理 SEM,包括:LISREL,AMOS, EQS, Mplus、 结构方程模型包括测量方程(LV 与 MV 之间关系得方程,外部关系)与结构方程(LV 之间关系得方程,内部关系),以 ACSI 模型为例,具体形式如下:测量方程 y=Λyη+εy , x=Λxξ+εx...