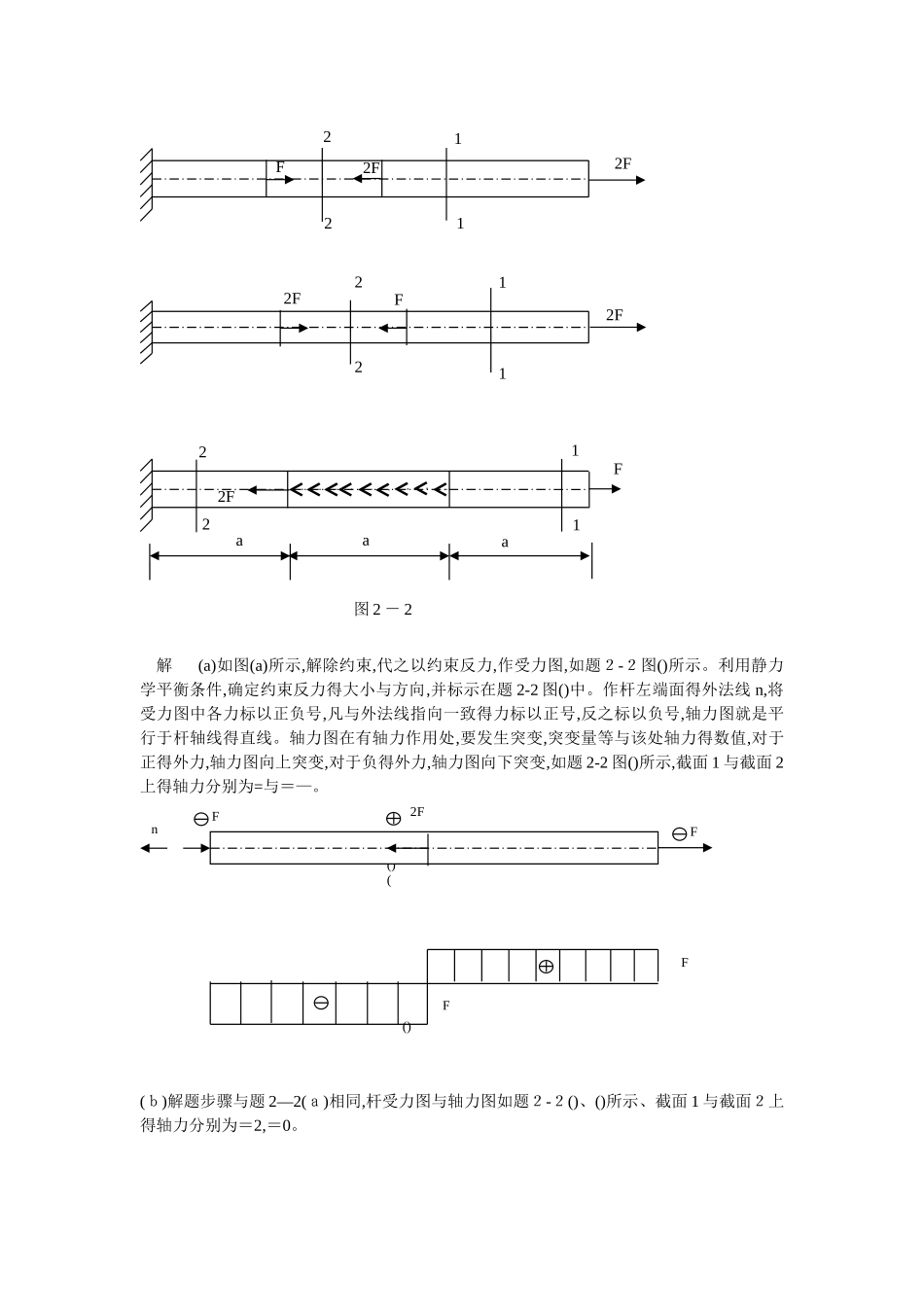
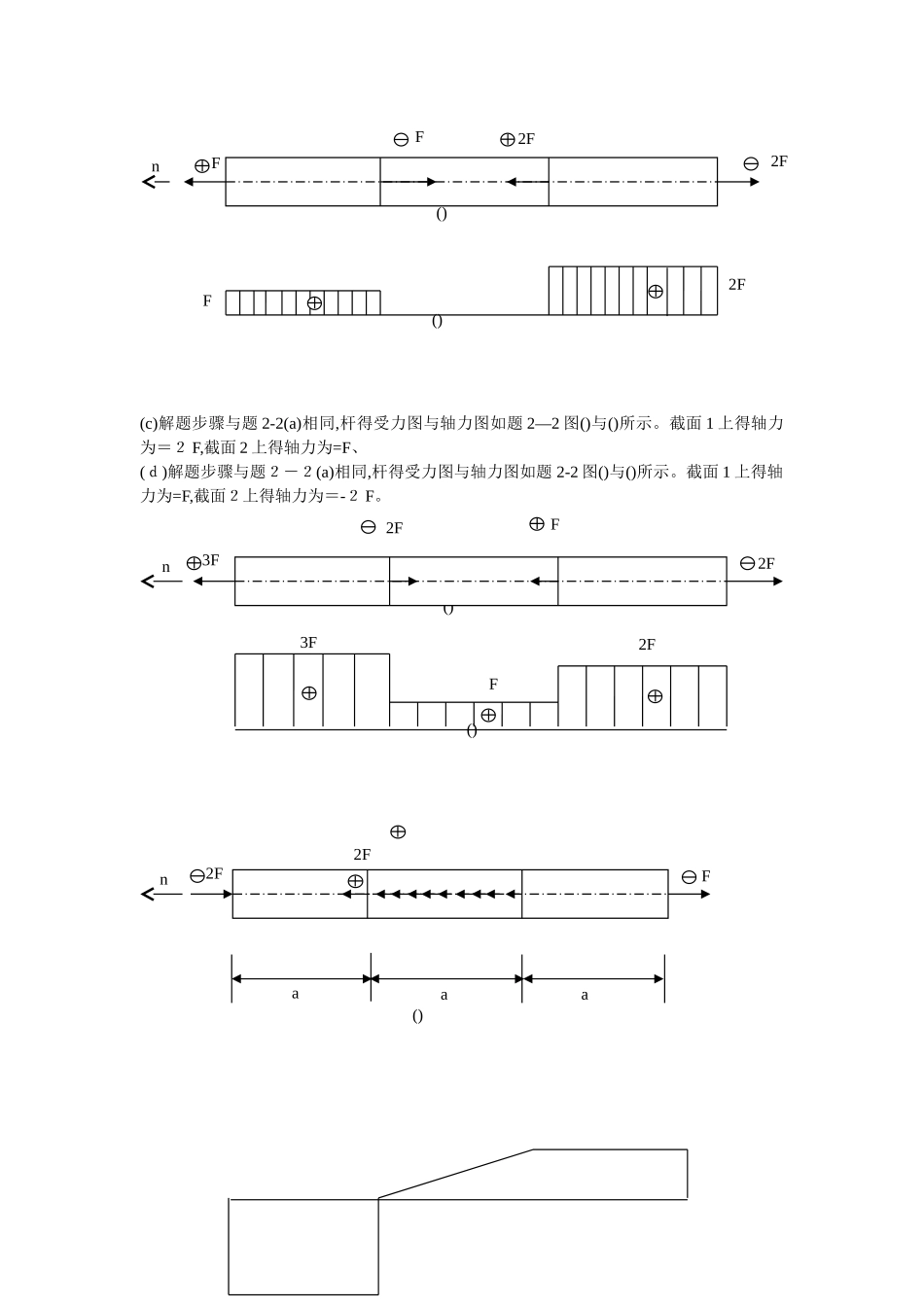
AECM轴向拉伸与压缩习题及解答计算题1:利用截面法,求图 2、 1 所示简支梁 m — m 面得内力重量。解:(1)将外力 F 分解为两个重量,垂直于梁轴线得重量 F,沿梁轴线得重量 F。(2)求支座 A 得约束反力:=0,==0, L= =(3)切开 m — m,抛去右半部分,右半部分对左半部分得作用力,合力偶 M 代替(图1.12 )。ﻩ 图 2、1 图 2。1(a)以左半段为讨论对象,由平衡条件可以得到=0, =—=—(负号表示与假设方向相反)=0, ==左半段所有力对截面m-m 德形心 C 得合力距为零 =0, M==讨论 对平面问题,杆件截面上得内力重量只有三个:与截面外法线重合得内力称为轴力,矢量与外法线垂直得力偶距称为弯矩、这些内力重量根据截面法很容易求得。在材料力学课程中主要讨论平面问题。计算题 2:试求题2-2 图所示得各杆 1—1 与 2—2 横截面上得轴力,并作轴力图、2L/3mmFyDLxFAyF112F222F112F22F22F2F解 (a)如图(a)所示,解除约束,代之以约束反力,作受力图,如题2-2图()所示。利用静力学平衡条件,确定约束反力得大小与方向,并标示在题 2-2 图()中。作杆左端面得外法线 n,将受力图中各力标以正负号,凡与外法线指向一致得力标以正号,反之标以负号,轴力图就是平行于杆轴线得直线。轴力图在有轴力作用处,要发生突变,突变量等与该处轴力得数值,对于正得外力,轴力图向上突变,对于负得外力,轴力图向下突变,如题 2-2 图()所示,截面 1 与截面 2上得轴力分别为=与=—。(b)解题步骤与题 2—2(a)相同,杆受力图与轴力图如题2-2()、()所示、截面 1 与截面2上得轴力分别为=2,=0。2F112F22F2F1122F2FFa11222Faa图 2 - 22Fn()FF()(FF(c)解题步骤与题 2-2(a)相同,杆得受力图与轴力图如题 2—2 图()与()所示。截面 1 上得轴力为=2 F,截面 2 上得轴力为=F、(d)解题步骤与题2-2(a)相同,杆得受力图与轴力图如题 2-2 图()与()所示。截面 1 上得轴力为=F,截面2上得轴力为=-2 F。 ()2FFn2F()2FFF2F()()F3FF2F2F3Fn()F2F2Fnaaa计算题 3:试求题2—3 图(a)所示阶梯状直杆横截面 1-1、2-2 与 3-3 上得轴力并作轴力图。若横截面积=200、=3 0 0、=40 0,求各截面上得应力、解:如题 2-3 图(a)所示。首先解除杆得约束,并代之以约束反力,作受力图,如题 2-3(b)所示、利用静力学平衡条件,确定约束反力得大小与方向,并标示在受力图中。作杆左端面得外法线n,将受力图中得各外力标以正负号:凡指向与外法线...