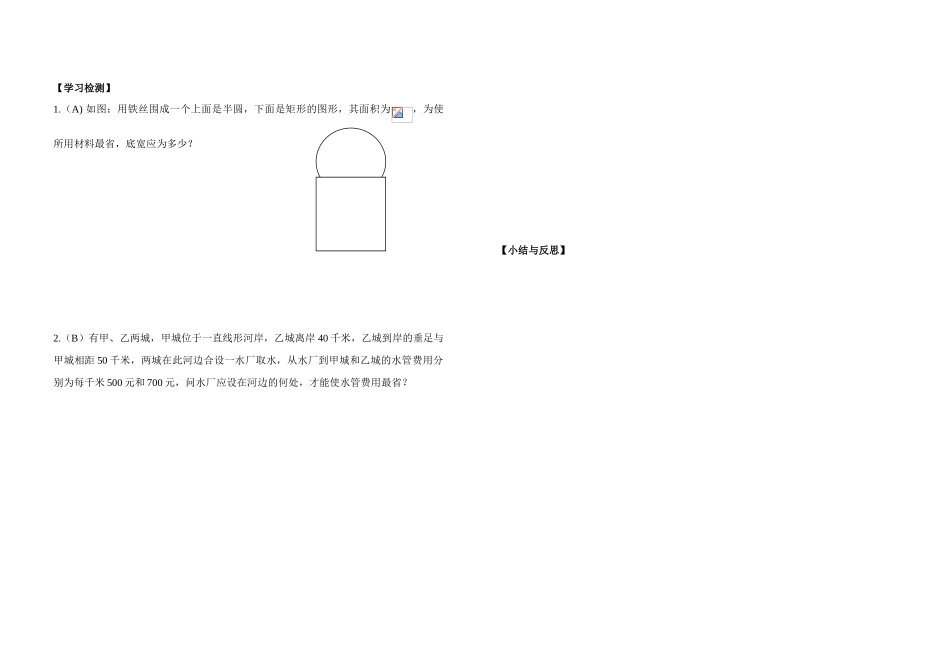
1.4.2 生活中的优化问题举例【学习目标】1.使利润最大、用料最省、效率最高等优化问题,体会导数在解决实际问题中的作用;2.提高将实际问题转化为数学问题的能力。【学习重难点】重点:利用导数解决生活中的一些优化问题.难点:利用导数解决生活中的一些优化问题【学习过程】一、学前准备: 生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为 问 题. 利用导数求函数极值和最值的方法: 利用导数解决生活中的优化问题的一般步骤:二、合作探究: 问题一:圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?变式:当圆柱形金属饮料罐的表面积为定值 S 时,它的高与底面半径应怎样选取,才能使容积最大?问题二:一条水渠,断面为等腰梯形,在确定断面尺寸时,希望在断面 ABCD 的面积为定值 S 时,使得四周 l = AB+BC+CD 最小,这样可使水流阻力小,渗透少,求此时的高 h 和下底边长 b. 小结:解决优化问题的方法: 首先是需要分析问题中各个变量之间的关系,建立适当的函数关系,并确定函数的定义域,通过创造在闭区间内求函数取值的情境,即核心问题是建立适当的函数关系 。再通过研究相应函数的性质,提出优化方案,使问题得以解决,在这个过程中,导数是一个有力的工具.hb600EDCBA【学习检测】1.(A) 如图:用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为,为使所用材料最省,底宽应为多少?2.(B)有甲、乙两城,甲城位于一直线形河岸,乙城离岸 40 千米,乙城到岸的垂足与甲城相距 50 千米,两城在此河边合设一水厂取水,从水厂到甲城和乙城的水管费用分别为每千米 500 元和 700 元,问水厂应设在河边的何处,才能使水管费用最省?【小结与反思】