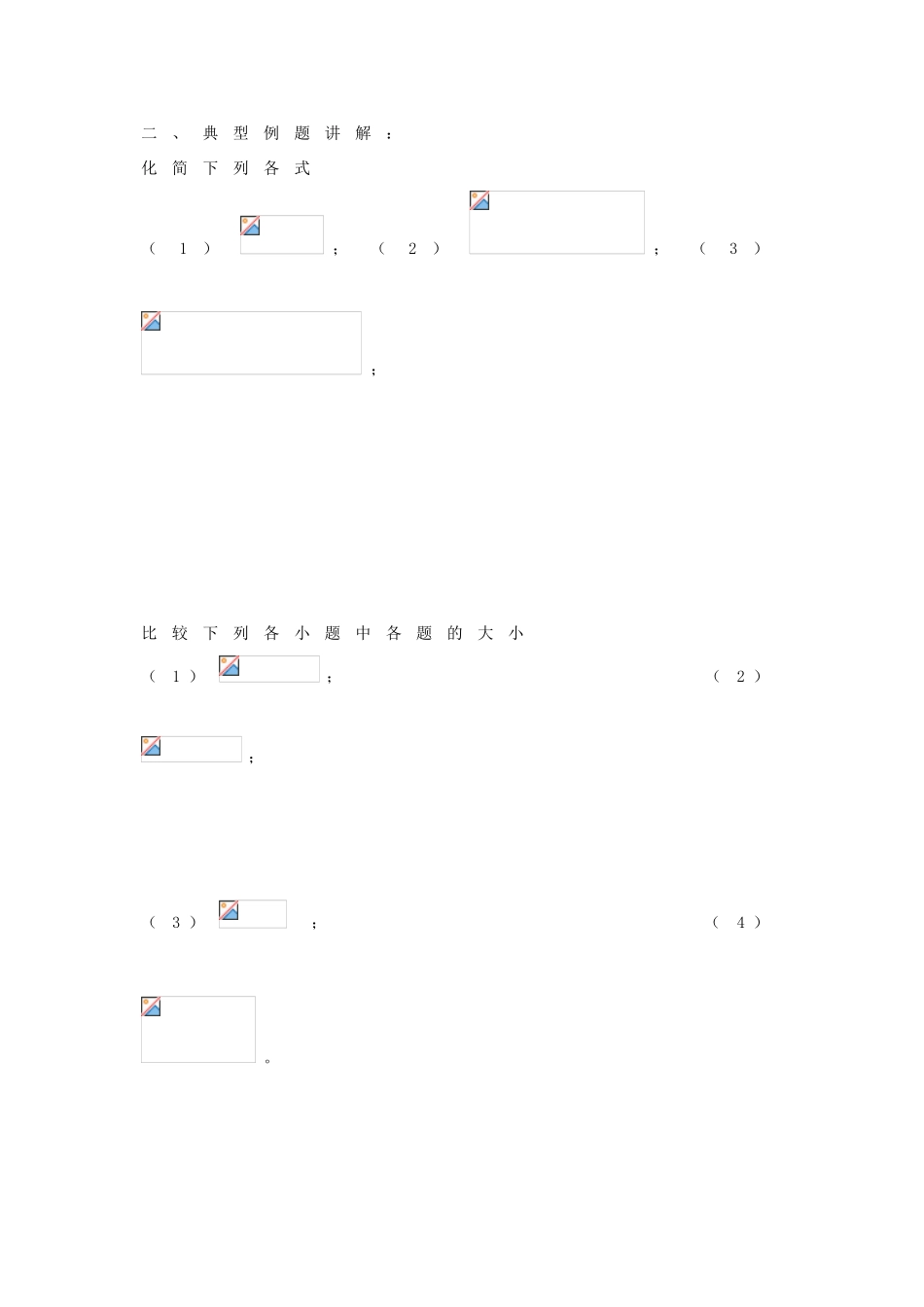
指 数 与 指 数 函 数 学 案一、知识点归纳根式:(1)根式的定义:如果_________ ,使得,则x 叫做___________的n 次方根。求的n 次方根,叫做把开n 次方,称作_____________。叫做根式,n 叫做_________ 。_________ 没有偶次方根。(2 )根式的性质:① ___________(____________) ② ③零的任何次方根都是_________ 。2 、指数幂的有关概念(1 )正整数指数幂:_________=;(2 )零指数幂:________ ; (3 )负整数指数幂:________ ;(4 )正分数指数幂:_______ ; (5 )负分数指数幂:________;(6 )0 的正分数指数幂等于________ ,0 的负分数指数幂________。3 、有理指数幂的性质:设对任意有理数,有理数指数幂的三条运算法则:(1)____________;(2)____________;(3 )____________ 。4 、指数函数的图象和性质定义___________叫做指数函数定义域______ _____值域___________图象性质(1 )___________;(2 )图象经过___________点;(3 )当__________ 时,;当__________时,;当__________ 时,;当__________ 时,。(4 )为增函数,为__________ 。(5 )___________________。二、典型例题讲解:化简下列各式(1);(2);(3);比较下列各小题中各题的大小(1 ); (2 );(3 ) ; (4 )。例3 、不等式的解集是___________________.例4 、已知函数。(1 )若,求的单调区间;(2 )若有最大值3 ,求的值。