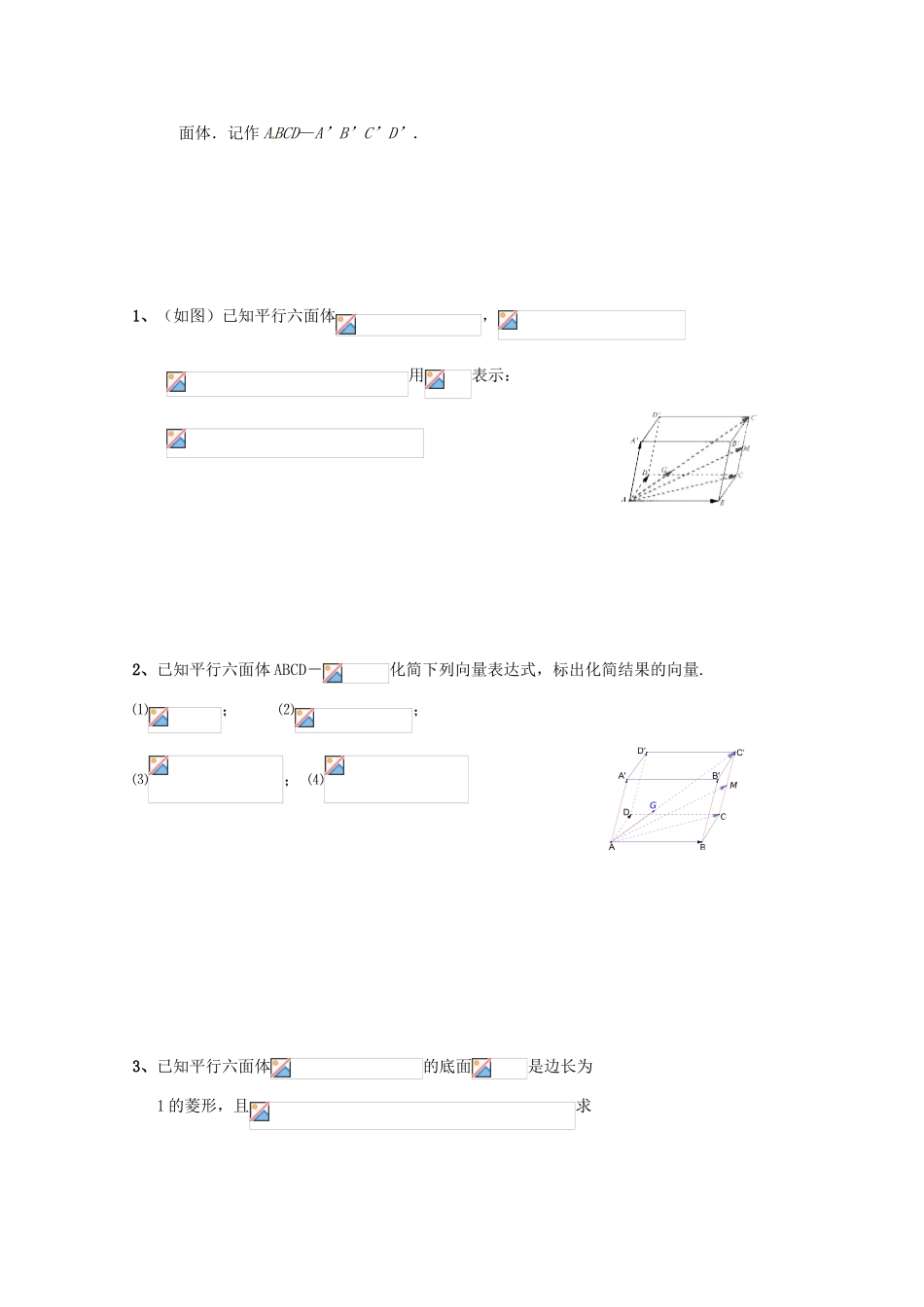
2.2 空间向量的运算学习目标:(空间向量;⒉相等的向量;⒊空间向量的加减与数乘运算及运算律学习重点:空间向量的加减与数乘运算及运算律学习难点:应用向量解决立体几何问题.学习过程:一、新旧知识连接:⑴ 怎样的向量叫做共线向量?⑵ 两个向量共线的充要条件是什么?⑶ 空间中点在直线上的充要条件是什么?二、我能自学:1.定义:求两个向量的和的运算,叫做向量的加法。注意:两个向量的和仍旧是向量(简称和向量); 2.向量加法的三角形法则与平行四边形法则;3. 向量加法运算律;4. 相反向量及向量减法的运算法则;三、.认识向量运算律及几何表示 加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 数乘分配律:λ(a+b)=λa+λb数乘分配律:λ(a + b) =λa +λb. ⑴ 首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:⑵ 首尾相接的若干向量若构成一个封闭图形,则它们的和为零向量.即:.⑶ 两个向量相加的平行四边形法则在空间仍然成立.因此,求始点相同的两个向量之和时,可以考虑用平行四边形法则. (4)平行四边形 ABCD 平移向量 a 到 A’B’C’D’的轨迹所形成的几何体,叫做平行六GMC'B'A'D'DABC面体.记作 ABCD—A’B’C’D’.1、(如图)已知平行六面体, 用表示:2、已知平行六面体 ABCD-化简下列向量表达式,标出化简结果的向量.⑴; ⑵;⑶; ⑷3、已知平行六面体的底面是边长为 1 的菱形,且求