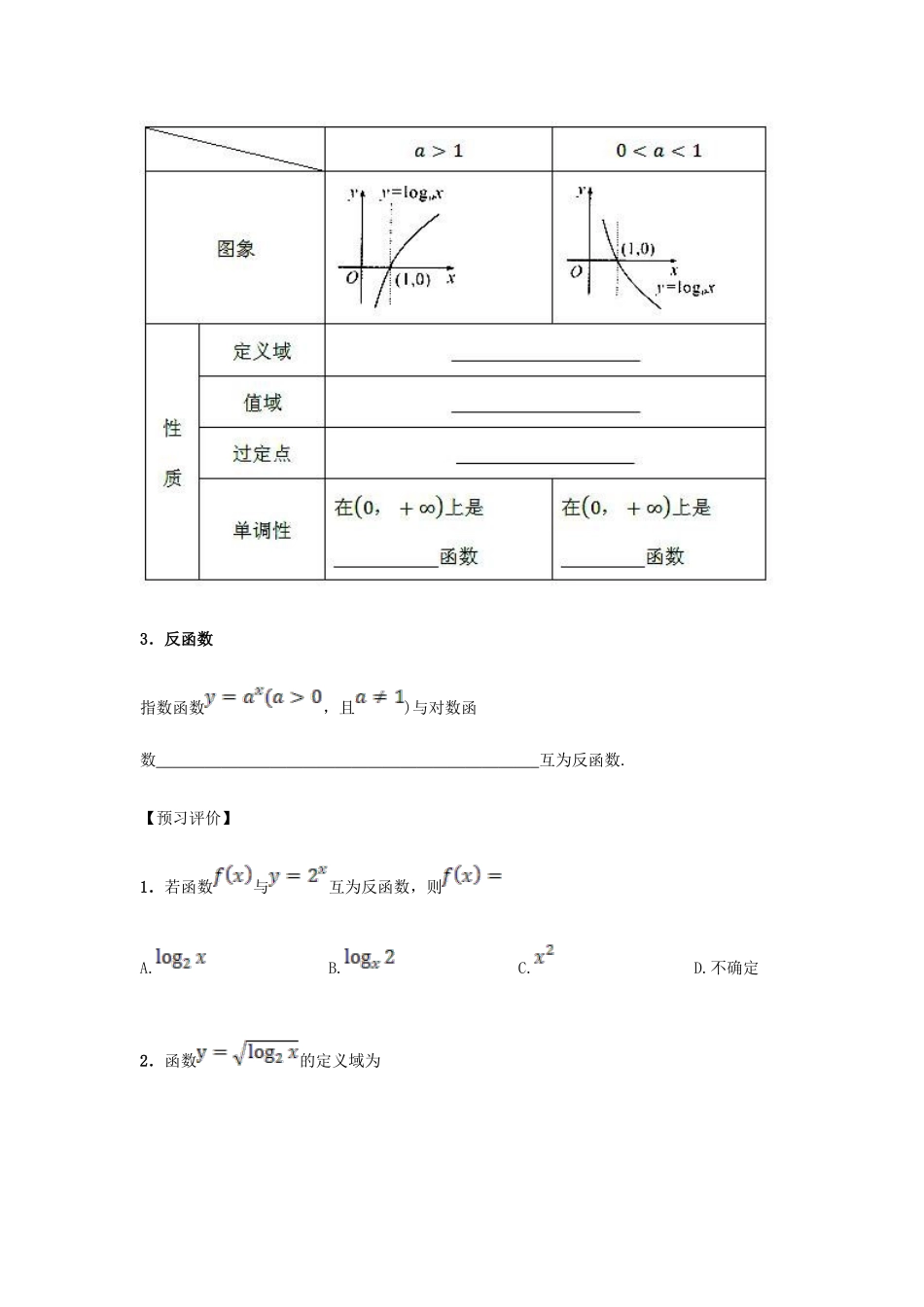
2.2.2 对数函数及其性质班级:__________姓名:__________设计人__________日期__________课前预习 · 预习案【温馨寄语】你有涌泉一样的智慧和一双辛勤的手,不管你身在何处,幸运与快乐时刻陪伴着你!【学习目标】1.理解对数函数的定义和意义.2.了解反函数的概念.3.掌握对数函数的图象和性质.【学习重点】对数函数的图象与性质【学习难点】对数函数的图象与性质【自主学习】1.对数函数的定义(1)解析式为: . (2)自变量是: .2.对数函数的图象和性质3.反函数指数函数,且)与对数函数 互为反函数.【预习评价】1.若函数与互为反函数,则A. B. C. D.不确定2.函数的定义域为A.(1,+∞) B. C.(-∞,1) D.3.对数函数与的图象如图,则A. B.C. D.4.已知函数,则的值为 .5.若对数函数的图象经过点(8,3),则函数的解析式为 .6.对数函数在定义域内是减函数,则的取值范围是 .知识拓展 · 探究案【合作探究】1.对数函数的图象与性质 (1)在同一坐标系内画出函数和的图象.并说出函数图象从左到右的变化趋势.(2)在问题(1)所画图象的基础上,现画出函数和的图象,观察所画出的两个函数图象的变化趋势及这四个函数图象的特征,回答下列问题:① 函数和的图象从左到右的变化趋势是怎样的?② 函数和的图象间有什么关系?和呢?③ 观察所画出的四个函数的图象,请说出对数函数图象的大致走势有几种?主要取决于什么?2.对数函数的解析式 请你根据所学过的知识,思考对数函数解析式中的底数能否等于0 或小于 0?3.对数函数的解析式 根据对数函数的解析式,完成下列填空,并明确其具有的三个结构特征(1)特征 1:底数 曾大于 0 且不等于 1 的 ,不含有自变量 .(2)特征 2:自变量 的位置在 ,且 的系数是 .(3)特征 3:的系数是 .【教师点拨】1.对数函数值的变化规律(1)(2)2.对对数函数图象与性质的三点说明(1)定点:所有对数函数的图象均过定点(1,0).(2)对称性:底数互为倒数的对数函数图象关于 轴对称.(3)图象随底数变化规律:在第一象限内,底数自左向右依次增大.3.确定对数函数解析式的关键确定对数函数解析式的关键是确定底数 的值.4.对对数函数一般形式的说明(1)定义中所说的形如的形式一般来说是不可改变的,否则就不是对数函数.(2)解析式中底数 取值范围为,其他范围都是不可以的.【交流展示】1.下列函数中是对数函数的是 .(1) .(2).(3).(4).(5).2.若对数函数的图象过点,求及.3.函数...