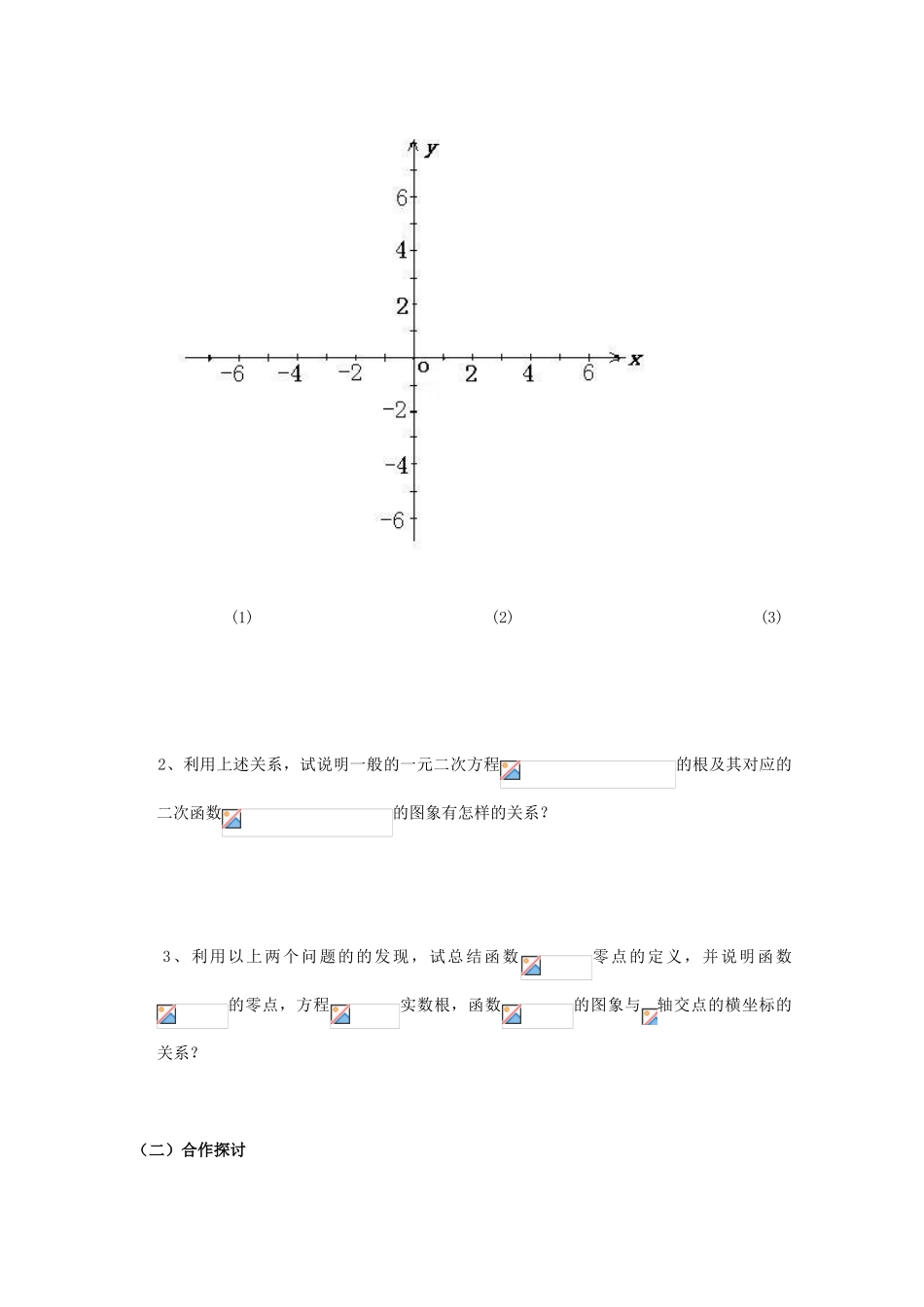
3.1.1 方程的根与函数的零点使用说明: “自主学习”15 分钟完成,出现问题,小组内部讨论完成,展示个人学习成果,教师对重点概念点评。 “合作探究”8 分钟完成,并进行小组学习成果展示,小组都督互评,教师重点点评。 “巩固练习”7 分钟完成,组长负责,小组内部点评。 “个人收获”5 分钟完成,根据个人学习和小组讨论情况,对掌握的知识点、方法进行总结,并找出理解不到位的问题。 最后 5 分钟,教师针对本节课中出现的重点问题做总结性点评。通过本节学习应达到如下目标: 1、理解函数(结合二次函数)零点的概念,领会函数零点与相应方程要的关系,掌握零点存在的判定条件.2、通过对零点定义的探究掌握零点存在性的判定方法.3、在函数与方程的联系中体验数学中的转化思想的意义和价值.学习重点:零点的概念及存在性的判定.学习难点:零点的确定.学习过程(一) 自主探究1、 观察下面几个一元二次方程及其相应的二次函数如:方程与函数方程与函数方程与函数(在下面坐标系中分别做出上述二次函数的图象,并解出的方程根 )试说明方程的根与图象与 x 轴交点的关系。 (1) (2) (3) 2、利用上述关系,试说明一般的一元二次方程的根及其对应的二次函数的图象有怎样的关系? 3、利用以上两个问题的的发现,试总结函数零点的定义,并说明函数的零点,方程实数根,函数的图象与轴交点的横坐标的关系?(二)合作探讨1、(Ⅰ)观察二次函数的图象 (见图 1) ,完成下面各小题。1) 在区间上有零点______; _______,_______,·_____0(<或>).2) 在区间上有零点______; ·____0(<或>).(Ⅱ)观察下面函数的图象(如图),完成下面各小题。1) 在 区 间上 ______( 有 / 无 ) 零 点 ; ·_____0(<或>). 2) 在区间上______(有/无)零点;·_____0(<或>).3) 区间上______(有/无)零点;·_____0(<或>).4) 区间上______(有/无)零点;有 个零点;·_____0(<或>).由以上几步探索,可以得出什么样的结论?2、(根的存在性定理): 在根的存在性定理中只须加入什么条件,零点的个数就是唯一的? 3、求函数的零点个数.(可以借助计算机或计算器来画函数的图象)(三)巩固练习1.利用函数图象判断下列方程有没有根,有几个根:(1); (2);(3); (4).2.利用函数的图象,指出下列函数零点所在的大致区间:(1); (2);(3); (4).(四) 个人收获与问题: 知识: 方法:问题:(五) 能力拓展:设函数。1) 利用计算机探求=2 和=3 时函数零点的个数。2) 当时,函数的零点是怎样分布的。