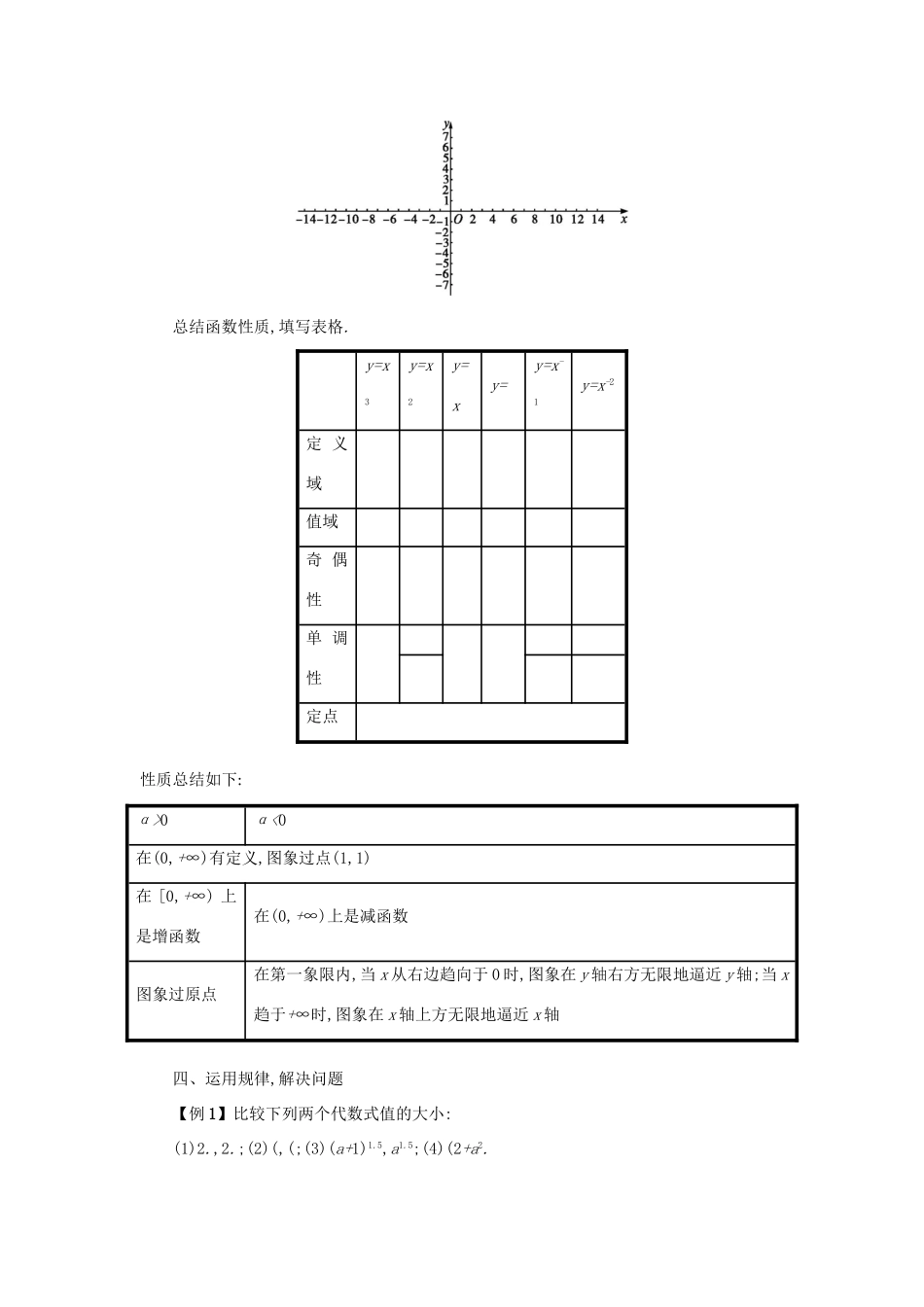
第二章 基本初等函数(Ⅰ)2.3 幂函数学习目标① 掌握幂函数的形式特征及具体幂函数的图象和性质;② 能应用幂函数的图象和性质解决有关的简单问题.合作学习一、设计问题,创设情境请看下列问题,并将每个问题中的 y 表示成 x 的函数.1.如果张红购买了每千克 1 元的水果 x 千克,那么她需要支付 y= (x>0)元; 2.如果正方形的边长为 x,那么正方形的面积 y= (x>0); 3.如果立方体的边长为 x,那么立方体的体积 y= (x>0); 4.如果一个正方形场地的面积为 x,那么这个正方形场地的边长 y= (x>0); 5.如果某人以 x m3/s 的速度向蓄水池注入了体积为 1m3 的水,那么他注水的时间 y= (x>0). 二、自主探索,尝试解决思考:1.以上是我们生活中经常遇到的几个数学模型,你能发现几个解析式结构上的共同特征吗?2.根据我们学习的函数的概念,你能不能判断它们能否构成函数?是我们学习过的哪类函数?如果不是,你能否根据该函数的特征给它起个恰当的名字?幂函数的定义(形式定义):请同学们举出一个具体的幂函数.三、信息交流,揭示规律y=x,y=x2,y=x3,y=,y=x-1,y=x-2.请同学们用描点法在平面直角坐标系中画出上述函数的图象.总结函数性质,填写表格.y=x3y=x2y=xy=y=x-1y=x-2定 义域值域奇 偶性单 调性定点性质总结如下:α>0α<0在(0,+∞)有定义,图象过点(1,1)在 [0,+∞) 上是增函数在(0,+∞)上是减函数图象过原点在第一象限内,当 x 从右边趋向于 0 时,图象在 y 轴右方无限地逼近 y 轴;当 x趋于+∞时,图象在 x 轴上方无限地逼近 x 轴四、运用规律,解决问题【例 1】比较下列两个代数式值的大小:(1)2.,2.;(2)(,(;(3)(a+1)1.5,a1.5;(4)(2+a2.【例 2】讨论函数 y=的定义域、奇偶性,作出它的图象,并根据图象说明函数的单调性.思考与讨论:幂函数 y=xα(α∈R),当 α=1,3,5,…(正奇数)时,函数有哪些性质?【例 3】证明幂函数 f(x)=在[0,+∞)上是增函数.五、变式演练,深化提高1.下列函数中,是幂函数的是( ) A.y=-B.y=3x2C.y=D.y=2x2.下列结论正确的是( )A.幂函数的图象一定过(0,0)和(1,1)B.当 α<0 时,幂函数 y=xα是减函数C.当 α>0 时,幂函数 y=xα是增函数D.函数 y=x2既是二次函数,也是幂函数3.函数 y=的图象大致是( )4.幂函数 y=的单调递增区间是 . 5.a=1.,b=0.,c=1.的大小关系是 . 6.幂函数 f(x)=a(m∈Z)的图象与 x 轴和 y 轴均无交点,并且图象关于原点对称,求 a 和m.六、反思小结,观点提炼1. 2. 3....