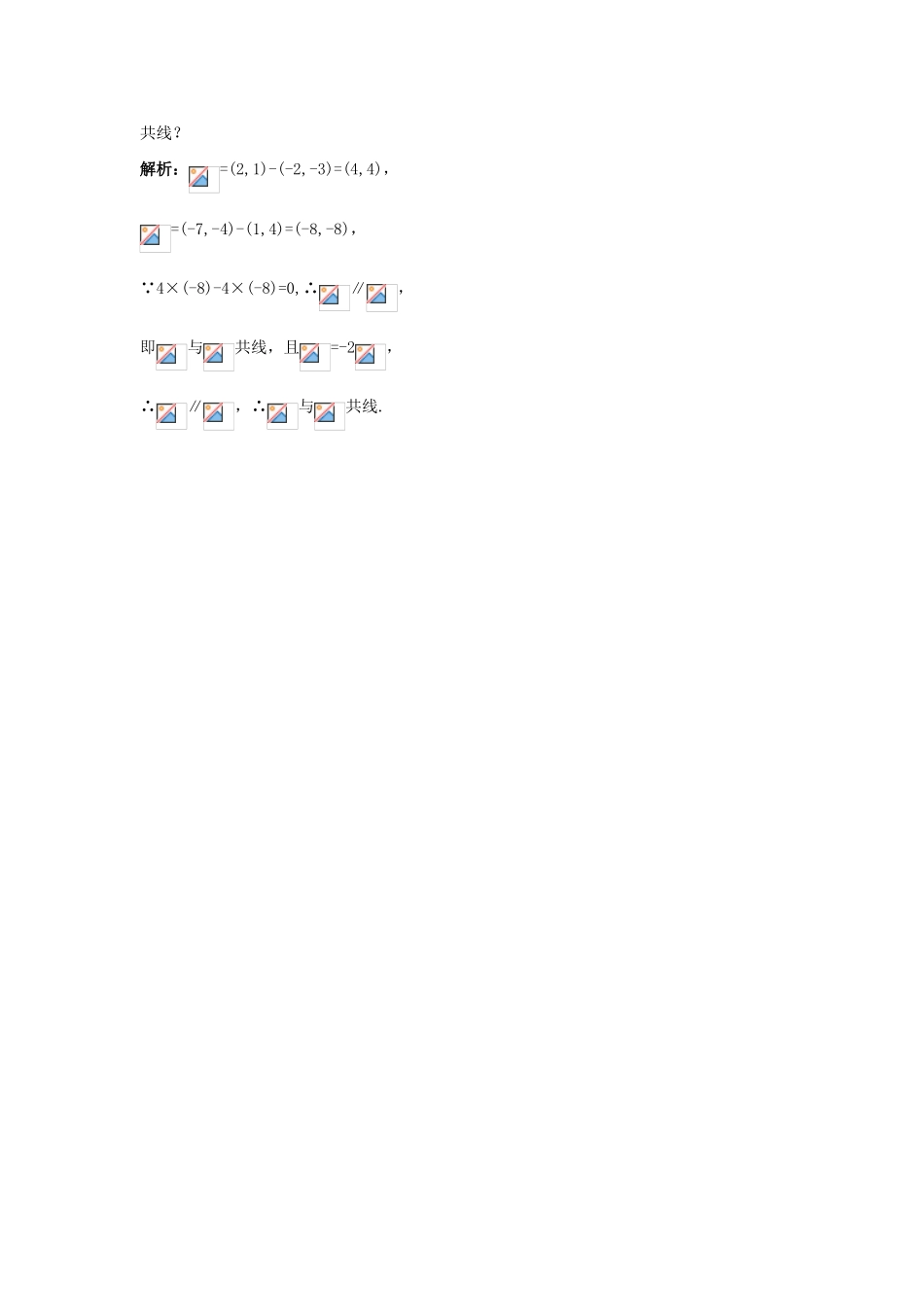
高中数学 2.3.2 平面向量的坐标运算第二课时互动课堂学案 苏教版必修 4疏导引导1.两向量平行的条件(1)设 a=(a1,a2),b=(b1,b2),则 a∥ba1b2-a2b1=0.(2)设 a=(a1,a2),b=(b1,b2),b 不平行于坐标轴,即 b1≠0,b2≠0,则 a∥b.用语言可以表述为:两个向量平行的条件是相应坐标成比例.2.两向量平行的条件的推导若 a∥b(b≠0) , 则 存 在 唯 一 实 数 λ, 使 a=λb. 反 之 , 如 果 存 在 一 个 实 数 λ 使a=λb(b≠0),则 a∥b.选择基底{e1,e2},如果 a=(a1,a2),b=(b1,b2),则条件 a=λb 可化为(a1,a2)=λ(b1,b2)=(λb1,λb2),即 a1=λb1,①a2=λb2.②①② 两式的两边分别乘以 b2,b1得a1b2=λb1b2,③a2b1=λb2b1.④③-④ 得 a1b2-a2b1=0.活学巧用【例 1】判断下列向量 a 与 b 是否平行:(1)a=(,),b=(-2,-3);(2)a=(0.5,4),b=(-8,64).解析:(1)×(-3)-(-2)=-+=0,∴a∥b.(2)0.5×64-4×(-8)=32+32=64≠0,∴ab.【例 2】已知 A(-2,-3),B(2,1),C(1,4),D(-7,-4),判断与是否共线?解析:=(2,1)-(-2,-3)=(4,4),=(-7,-4)-(1,4)=(-8,-8),∵4×(-8)-4×(-8)=0,∴∥,即与共线,且=-2,∴∥,∴与共线.