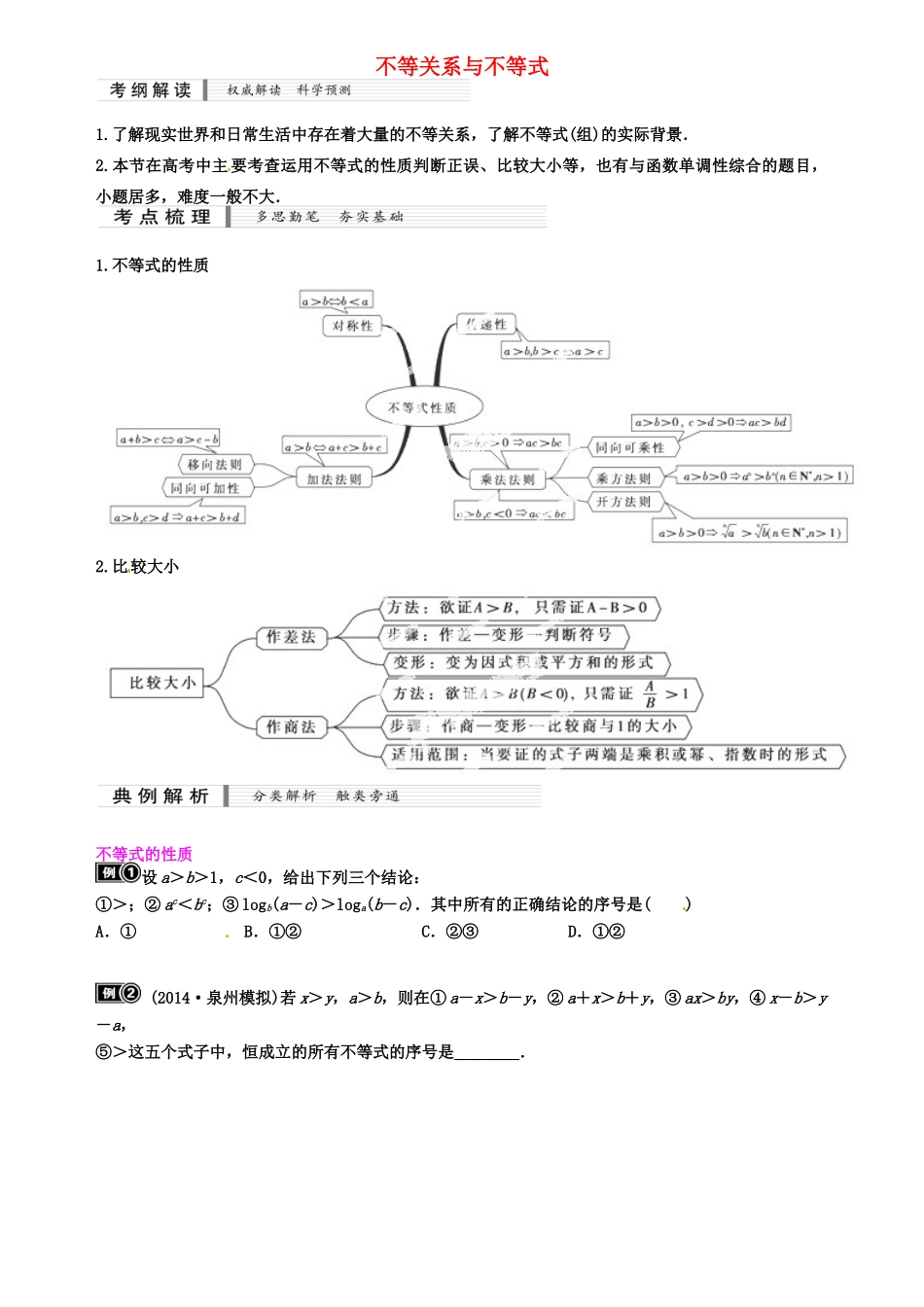
不等关系与不等式1.了解现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景.2.本节在高考中主 要考查运用不等式的性质判断正误、比较大小等,也有与函数单调性综合的题目,小题居多,难度一般不大.1.不等式的性质 2.比较大小 不等式的性质设 a>b>1,c<0,给出下列三个结论:①>;② ac<bc;③ logb(a-c)>loga(b-c).其中所有的正确结论的序号是( )A.① B.①②C.②③ D.①② (2014·泉州模拟)若 x>y,a>b,则在① a-x>b-y,② a+x>b+y,③ ax>by,④ x-b>y-a,⑤>这五个式子中,恒成立的所有不等式的序号是________. 若<<0,则下列不等式:①<;②|a|+b>0;③ a->b-;④ ln a2>ln b2中,正确的不等式是 不等式性质的应用 (1)若 1<α<3,-4<β<2,则-β 的取值范围是________. (2)已知-1<a+b<3 且 2<a-b<4,求 2a+3b 的取值范围. (1)若角 α,β 满足-<α<β<,则 2α-β 的取值范围是________. (2)设 f(x)=ax2+bx,且 1≤f(-1)≤2,2≤f(1)≤4,求 f(-2)的取值范围.比较大小 若 a=,b=,c=,则( ).A.a<b<c B.c<b<a C.c<a<b D.b<a<c 比较与(其中实数 b>a>0,实数 m>0)的大小. 1. 若 a<0,-1(-ab 2)-1;④0.5-a>0.5.2.(2012·四川卷)设 a,b 为正实数.现有下列命题:① 若 a2-b2=1,则 a-b<1;②若-=1,则 a-b<1;③若|-|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.其中的真命题有________(写出所有真命题的编号)两个防范 一是在使用不等式 时,一定要搞清它们成立的前提条件,不可强化或弱化成立的条件,如“同向不等式”才可相加、“同向且两边同正的不等式”才可相乘;“可乘性中的”c 的符号等都需注意.二是利用特值法判断两个式子大小时,错误的关系式,只需取特值举反例即可,而正确的关系式,则需推理论证.1.设 f(x)=3x2-x+1,g(x)=2x2+x-1,x∈R,则 f(x)与 g(x)的大小关系是( )A.f(x)>g(x) B.f(x)≥g(x) C.f(x)=g(x) D.f(x)<g(x)2.(2014·保定模拟)已知 a>b,则下列不等式成立的是( ).A.a2-b2≥0 B.ac>bcC.|a|>|b| D.2a>2b3.2014·河南三市三模)已知 0<a<1,x=loga+loga ,y=loga5,z=loga -loga ,则(...