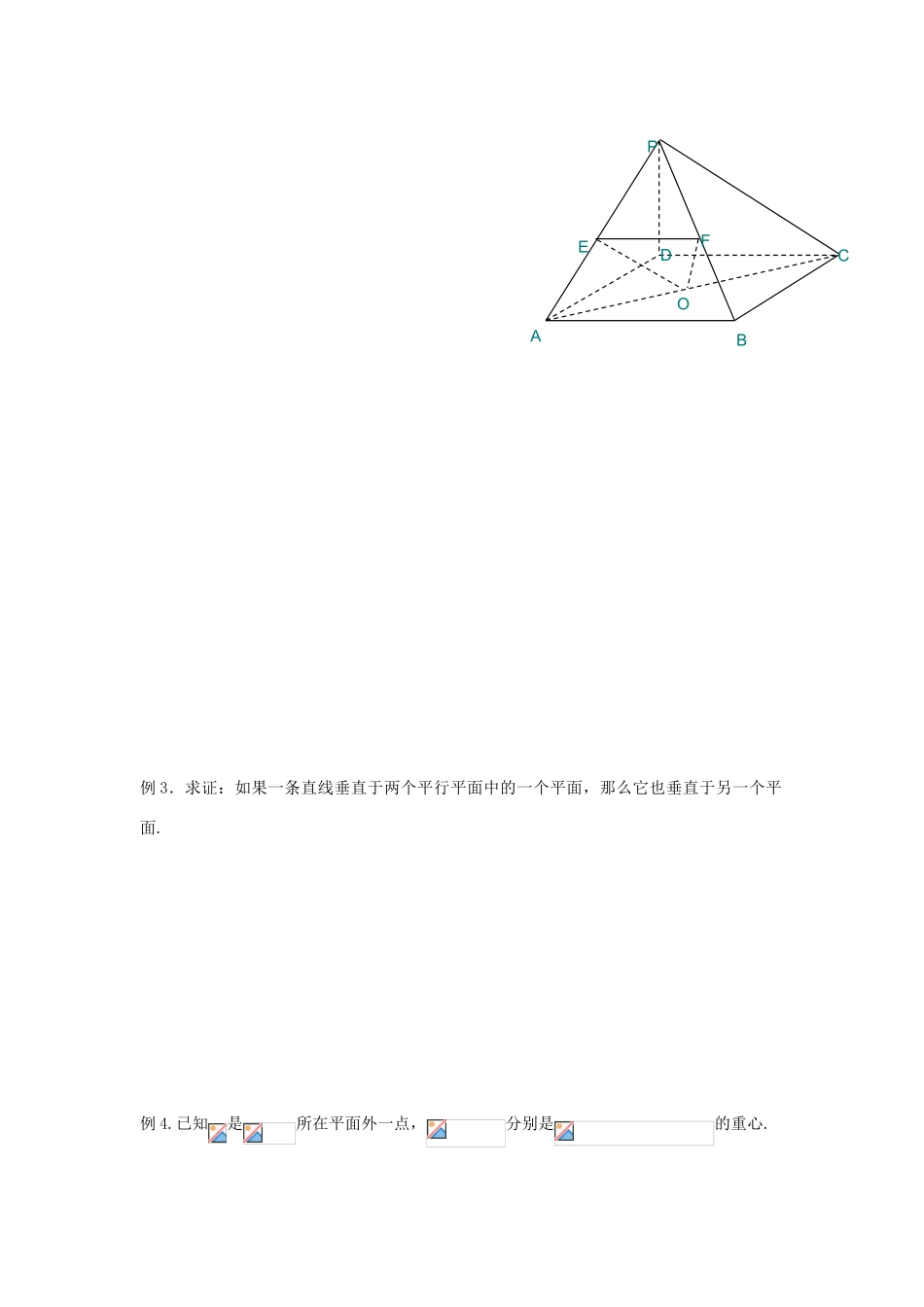
第 15 课时 两个平面平行的判定【学习目标】1、 了解空间面面平行的有关概念;2、 理解并能用图形语言和符号语言表述面面平行的判定定理;3、 会准确运用面面平行判定定理证明有关题目. 【问题情境】1.空间两个平面的位置关系:问题 1:空间两个平面有几种位置关系?问题 2:如何来定义两个平面相交和平行?问题 3:若两个平面有公共点,则公共点有几个?这些公共点有什么特点?注意:在作图中,要表示两个平面平行时,应把表示这两个平面的平行四边形画成对应边平行。2.两个平面平行的判定(1)根据定义(2)判定定理——把面面关系转化为线面关系思考:假定平面,那么,对于平面内的任意一条直线 m,它同平面有什么关系?问题 1:若平面内有一条直线,能否判定?为什么?位置关系两平面平行两平面相交公共点符号表示图形表示问题 2:若平面内有两条直线 m、n,,,能否判定?为什么?问题 3:将平面内有两条直线 m、n 限制为两条相交直线,情况又怎样?两个平面平行的判定定理表述为:文字语言符号语言 图形语言简记为问题 4:如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行吗?为什么?【合作探究】例 1.如图,在长方体 ABCD-A1B1C1D1 中,求证:平面 BC1D∥平面 AB1D1.思考:A1C 与平面 BC1D 垂直吗?为什么?例 2.如图所示,P 是正方形所在平面外的一点, O,E,F 分别为 AC,PA,PB 的中点,求证:平面 EOF//平面 PDC DABCA1D1C1B1例 3.求证:如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.例 4.已知是所在平面外一点,分别是的重心.PABCDEFO求证:‖平面.思考:垂直于同一条直线的两个平面平行吗?【学以致用】1、下列条件中,能判断两个平面平行的是 (1).一个平面内的一条直线平行于另一个平面;(2).一个平面内的两条直线平行于另一个平面;(3).一个平面内有无数条直线平行于另一个平面;(4).一个平面内任何一条直线都平行于另一个平面.2、若平面‖平面则直线的位置关系 3、如图 B 为ACD 所在平面外一点,M、N、G 分别为ABC、ABD、BCD 的重心,(1)求证:平面 MNG//平面 ACD;(2)求ABDCPHFMGN第 15 课时 同步训练1.若平面∥平面,直线 a ,直线 b,则在下面四种情况:①a∥b ②a⊥b ③a 与 b 异面 ④ a、b 相交其中可能出现的情况有 .2.在正方体 ABCD—A1B1C1D1中,P、Q 分...