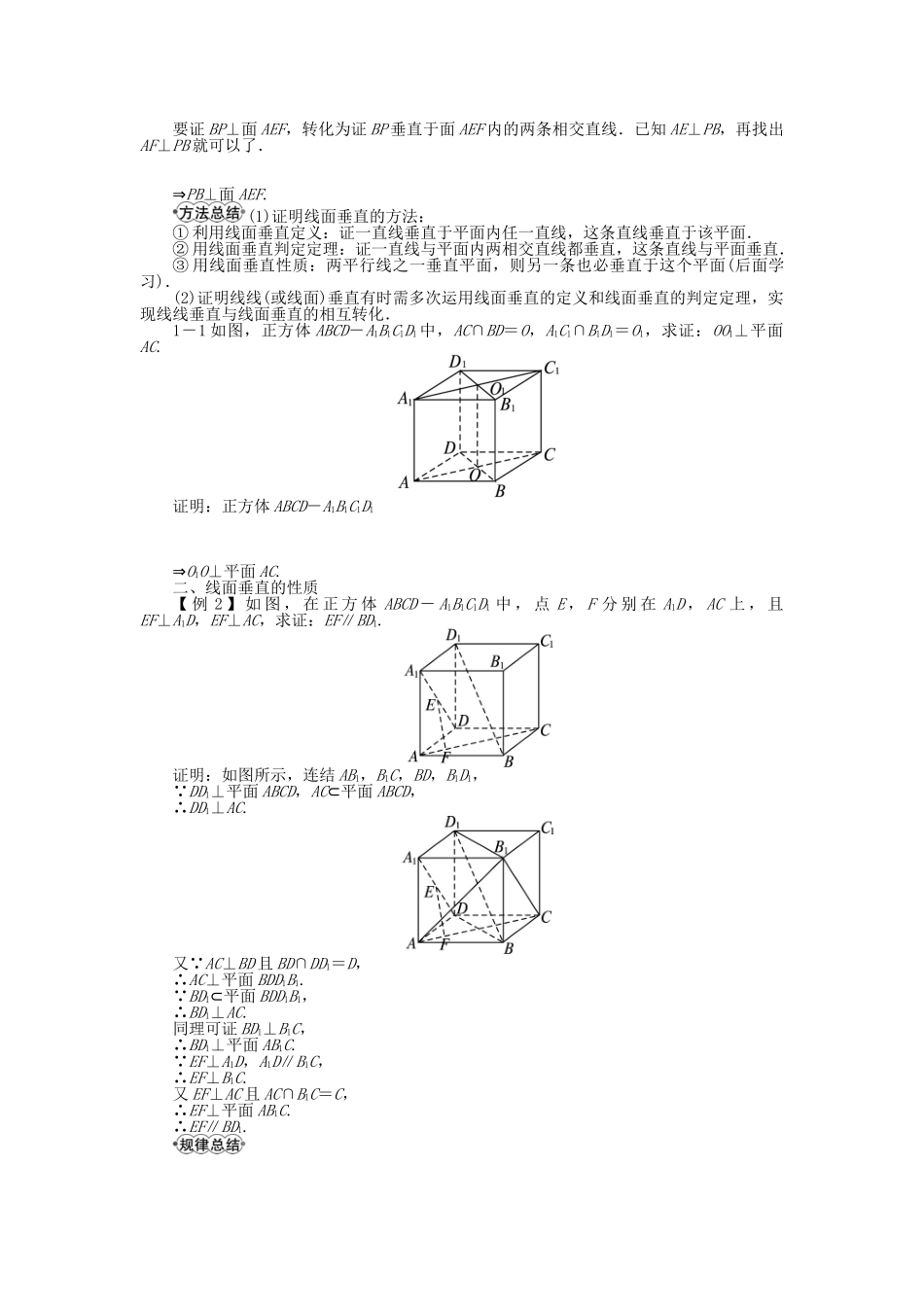
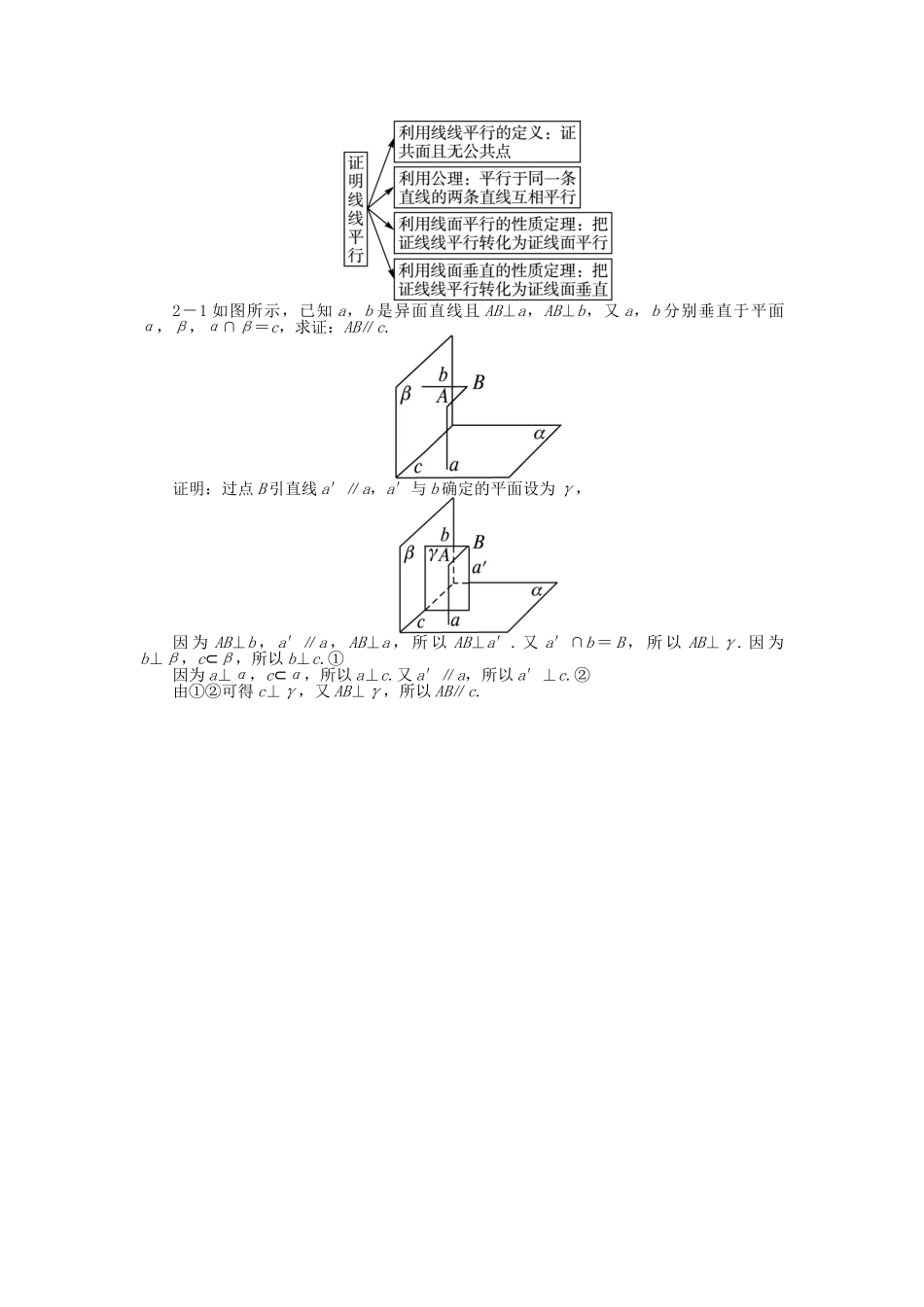
6.2.3 垂直关系(1)1.定义:如果一条直线与一个平面相交,并且垂直于这个平面内所有的直线,就称这条直线与这个平面垂直.这条直线叫作这个平面的垂线,这个平面叫作这条直线的垂面,它们的交点叫作垂足.2.设 a,b 是异面直线,过 a 上任意一点 A 作 c∥b,如果 a⊥c,就称 a⊥b.3.直线与平面垂直的判定与推论如下表.文字语言图形语言符号语言性质判定定理如果一条直线垂直于一个平面内的两条相交直线,那么这条直线就与这 个 平 面 垂直.⇒a ⊥ α ⇒a⊥m判定定理的推论两条平行直线中的一条垂直于一个平面,则另一条也垂直 于 这 个 平面.⇒b ⊥ α ⇒a ∥ b 直线 l 垂直于面 α 内的无数条直线,l 与面 α 垂直吗?提示:不一定垂直,如图所示.如果 l⊥a,l⊥b,l⊥c,…;a∥b∥c∥…;a,b,c,…⊂α.但 l 与 α 不垂直.4.定理 7(直线与平面垂直的性质定理):垂直于同一个平面的两条直线平行.一、线面垂直的判定【例 1】如图所示,AB 为圆 O 的直径,C 为圆 O 上的一点,PA⊥平面 ABC,AE⊥BP 于点E,AF⊥CP 于点 F,求证:BP⊥平面 AEF.要证 BP⊥面 AEF,转化为证 BP 垂直于面 AEF 内的两条相交直线.已知 AE⊥PB,再找出AF⊥PB 就可以了.⇒PB⊥面 AEF.(1)证明线面垂直的方法:① 利用线面垂直定义:证一直线垂直于平面内任一直线,这条直线垂直于该平面.② 用线面垂直判定定理:证一直线与平面内两相交直线都垂直,这条直线与平面垂直.③ 用线面垂直性质:两平行线之一垂直平面,则另一条也必垂直于这个平面(后面学习).(2)证明线线(或线面)垂直有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.1-1 如图,正方体 ABCD-A1B1C1D1 中,AC∩BD=O,A1C1∩B1D1=O1,求证:OO1⊥平面AC.证明:正方体 ABCD-A1B1C1D1⇒O1O⊥平面 AC.二、线面垂直的性质【 例 2 】 如 图 , 在 正 方 体 ABCD - A1B1C1D1 中 , 点 E , F 分 别 在 A1D , AC 上 , 且EF⊥A1D,EF⊥AC,求证:EF∥BD1.证明:如图所示,连结 AB1,B1C,BD,B1D1, DD1⊥平面 ABCD,AC⊂平面 ABCD,∴DD1⊥AC.又 AC⊥BD 且 BD∩DD1=D,∴AC⊥平面 BDD1B1. BD1⊂平面 BDD1B1,∴BD1⊥AC.同理可证 BD1⊥B1C,∴BD1⊥平面 AB1C. EF⊥A1D,A1D∥B1C,∴EF⊥B1C.又 EF⊥AC 且 AC∩B1C=C,∴EF⊥平面 AB1C.∴...