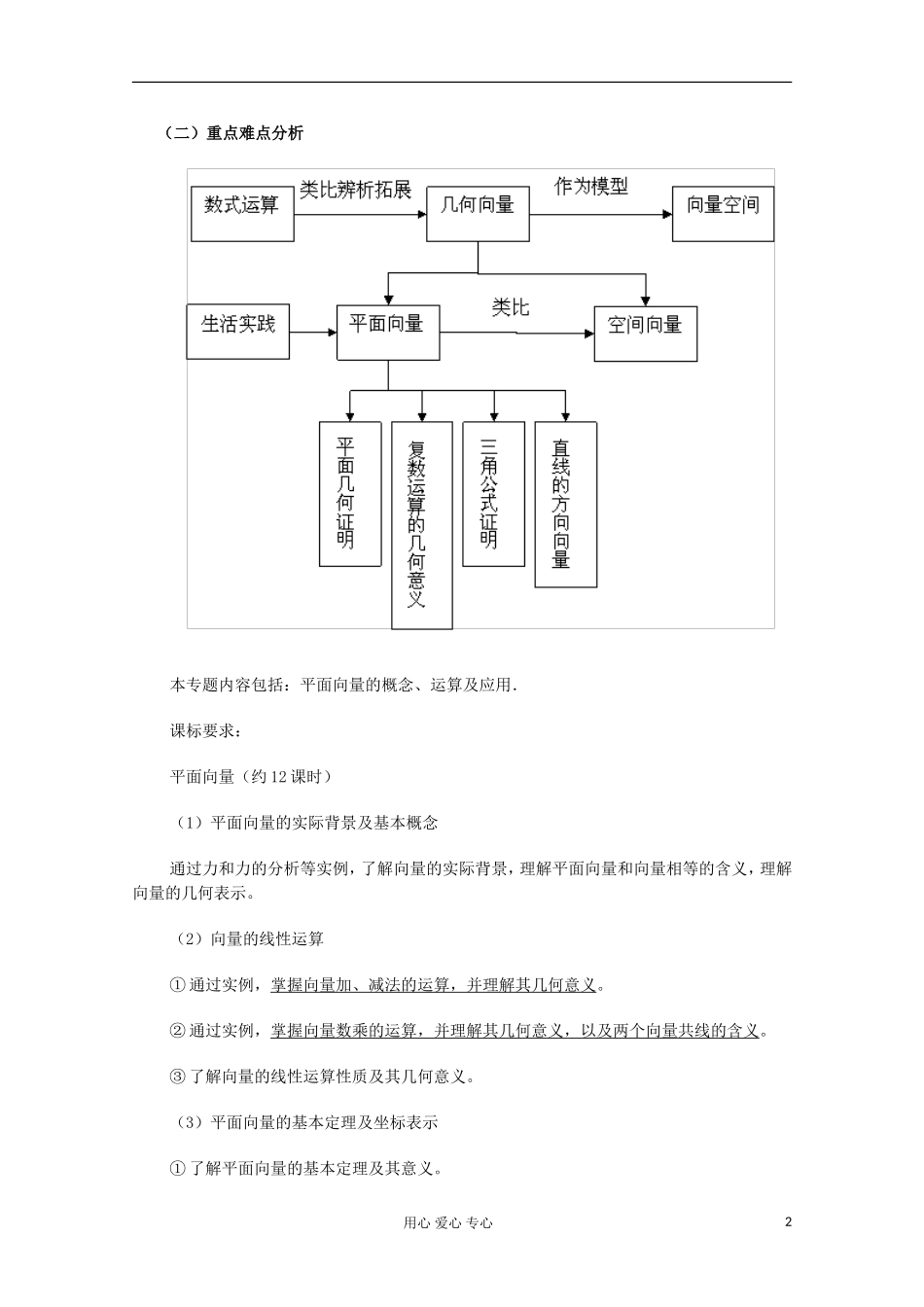
专题讲座高中数学“平面向量”教学研究 一、整体把握“平面向量”教学内容(一)平面向量知识结构图用心 爱心 专心1(二)重点难点分析本专题内容包括:平面向量的概念、运算及应用.课标要求:平面向量(约 12 课时)(1)平面向量的实际背景及基本概念通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示。(2)向量的线性运算① 通过实例,掌握向量加、减法的运算,并理解其几何意义。② 通过实例,掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义。③ 了解向量的线性运算性质及其几何意义。(3)平面向量的基本定理及坐标表示① 了解平面向量的基本定理及其意义。用心 爱心 专心2② 掌握平面向量的正交分解及其坐标表示。③ 会用坐标表示平面向量的加、减与数乘运算。④ 理解用坐标表示的平面向量共线的条件。(4)平面向量的数量积① 通过物理中“功”等实例,理解平面向量数量积的含义及其物理意义。② 体会平面向量的数量积与向量投影的关系。③ 掌握数量积的坐标表达式,会进行平面向量数量积的运算。④ 能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系。(5)向量的应用经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程,体会向量是一种处理几何问题、物理问题等的工具,发展运算能力和解决实际问题的能力。依据课标要求,并结合前面的分析可知:新概念、新运算的定义,向量运算和向量运算的几何意义是本专题的重点,平面向量基本定理是坐标表示(几何代数化)的关键,也是本专题教学的难点。二、“平面向量”教与学的策略(一)在概念教学中,依据概念教学的方法,建构概念知识体系本专题的教学中,向量、向量的运算等都是新定义的概念,如何让这些概念的出现自然轻松,还能让学生迅速把握住本质,达成理解?不妨遵循概念教学的方法。比如说:“向量的概念”教学中,可从力、位移等实例引入,进行抽象概括,形成向量的概念。之后,提出“温度、功是不是向量?”这样的问题,通过比较,对向量的概念进行辨析,在此基础上,抓住向量的两个要点:大小、方向进行拓展,按如下表格整理,将向量概念精致化。用心 爱心 专心3概念辨析:本专题的内容中,学生的问题之一是:概念不清,符号表示混乱,针对此问题,一方面教师在板书、表达等方面一定要准确和多方强调,另一方面,也可设置一些判断题,帮助学生...