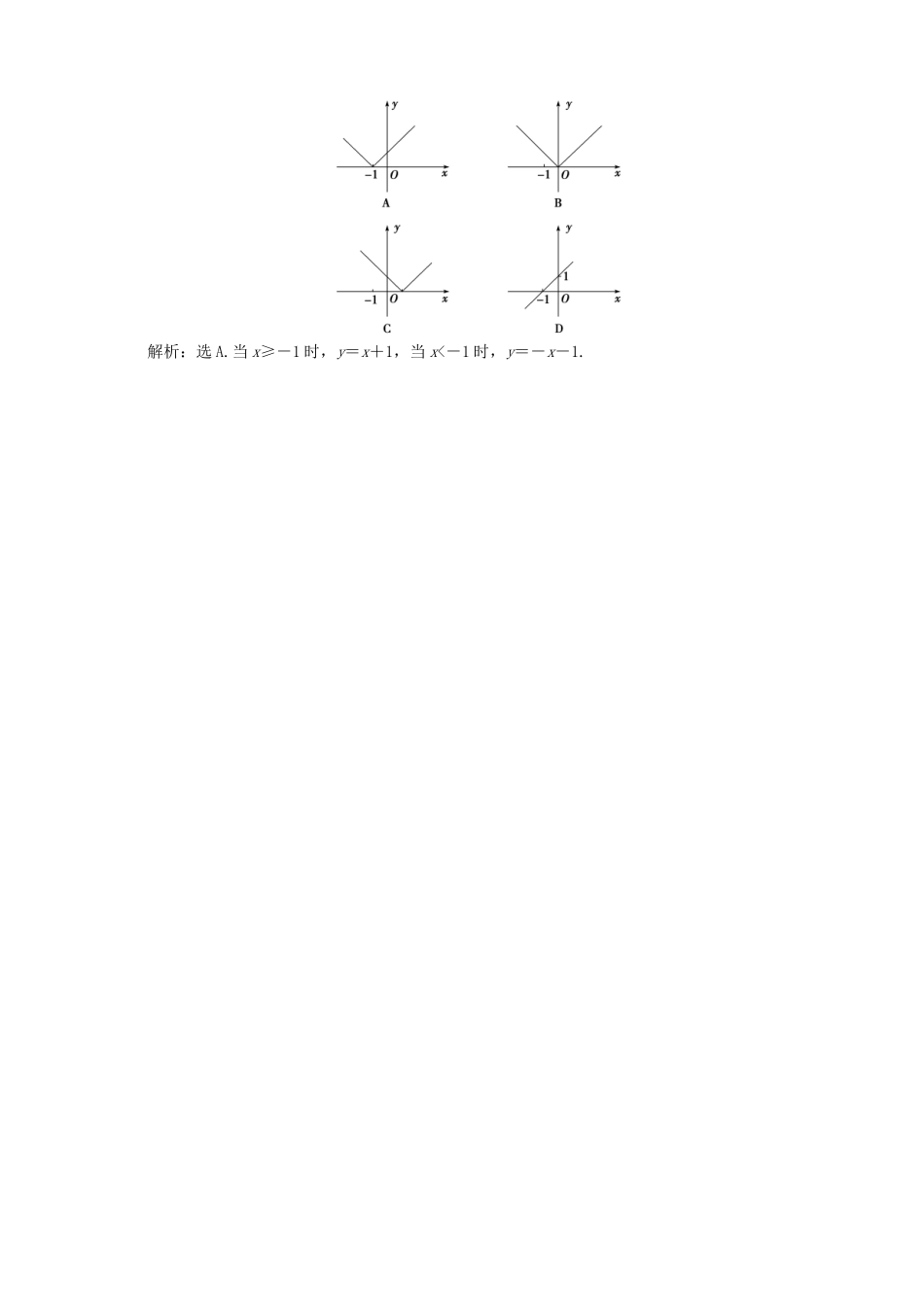
第 2 课时 函数的图象 1.了解图象法是表示函数关系的重要方法. 2.掌握描点法作图及应用图象比较函数值大小的方法. [学生用书 P18]函数的图象将自变量的一个值 x0作为横坐标,相应的函数值 f(x0)作为纵坐标,就得到坐标平面上的一个点( x 0, f ( x 0)),当自变量取遍函数定义域 A 中的每一个值时,就得到一系列这样的点,所有这些点组成的集合(点集)为{(x,f(x))|x∈A},即{(x,y)|y=f(x),x∈A},所有这些点组成的图形就是函数 y=f(x)的图象.1.判断(正确的打“√”,错误的打“×”)(1)任何一个函数都可以用图象表示.( )(2)函数 f(x)=2x+1(10)在第一象限的部分,直线 y=(x<0)在第二象限的部分和点(0,1)三部分合在一起构成,如图所示.(2)f(1)=12=1,f(0)=1,f(-3)=,f[f(-3)]=f=,f{f[f(-3)]}=f=f=. 函数图象的画法[学生用书 P18] 作出下列函数的图象.(1)y=1+x(x∈Z);(2)y=x2-2x(x∈[0,3)).【解】 (1)这个函数的图象由一些点组成,这些点都在直线 y=1+x 上,如图(1)所示.(2)因为 x∈[0,3),所以这个函数的图象是抛物线 y=x2-2x 在 0≤x<3 之间的一段弧,如图(2)所示.利用描点法作函数图象的基本步骤→→→→ 1.作出下列函数的图象.(1)y=x2+x(-1≤x≤1);(2)y=(-2≤x≤2,且 x≠0).解:如图: 函数图象的识辨[学生用书 P19] 已知函数 y=|x|+1,则其图象是( )【解析】 由 y=|x|+1 可知,|x|≥0,所以|x|+1≥1,所以 y≥1,所以 C 正确.【答案】 C函数的图象可以反映函数的有关特点,如定义域、值域,通过比较一些特殊点,我们可以判断函数图象的大致趋势. 2.函数 y=|x+1|的图象为( )解析:选 A.当 x≥-1 时,y=x+1,当 x<-1 时,y=-x-1. 函数图象的应用[学生用书 P19] 作出下列函数的图...