高中数学 第2章 函数章末复习课学案 北师大版必修1-北师大版高一必修1数学学案

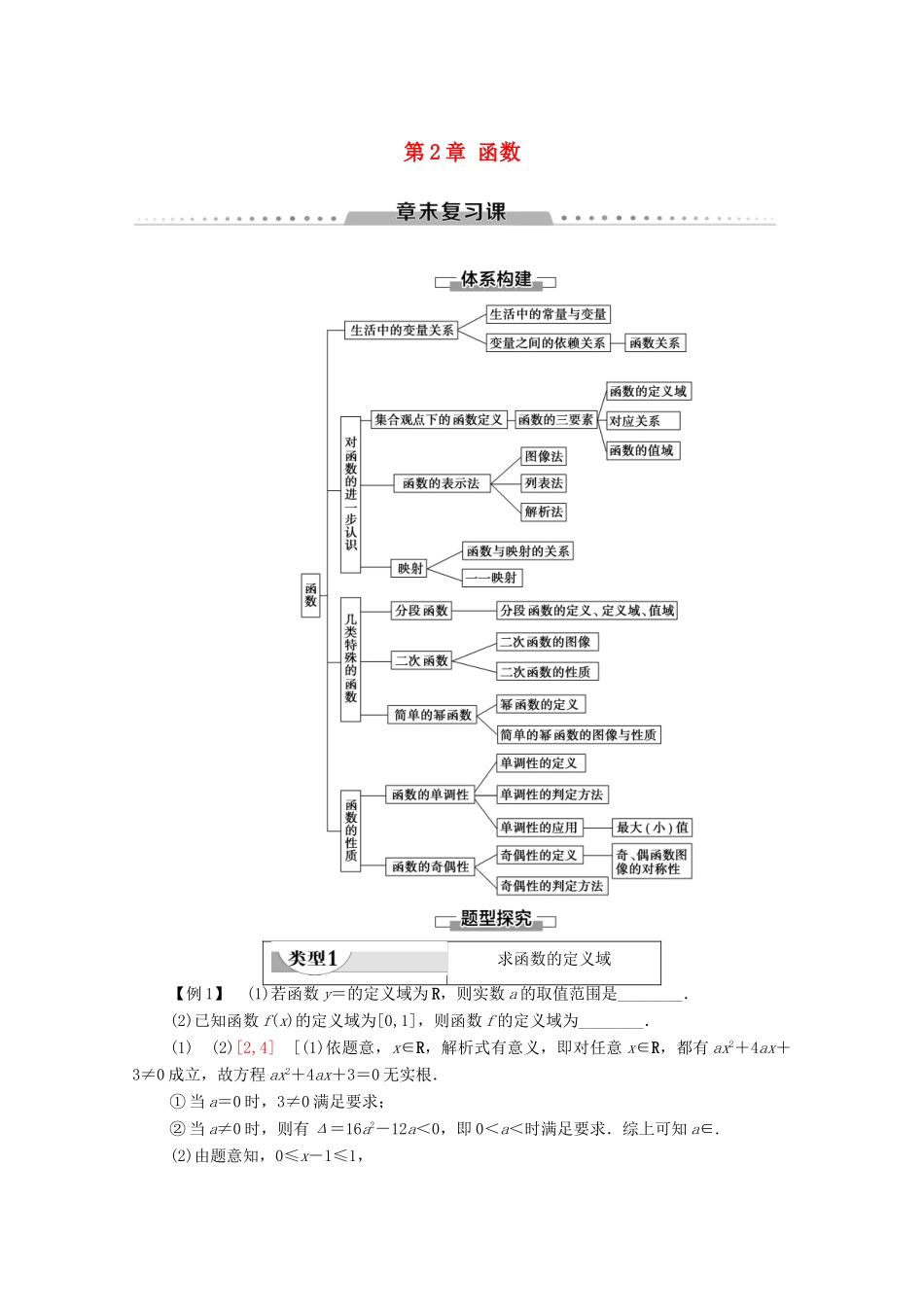
第 2 章 函数求函数的定义域【例 1】 (1)若函数 y＝的定义域为 R，则实数 a 的取值范围是________．(2)已知函数 f(x)的定义域为[0,1]，则函数 f 的定义域为________．(1) (2)[2,4] [(1)依题意，x∈R，解析式有意义，即对任意 x∈R，都有 ax2＋4ax＋3≠0 成立，故方程 ax2＋4ax＋3＝0 无实根．① 当 a＝0 时，3≠0 满足要求；② 当 a≠0 时，则有 Δ＝16a2－12a＜0，即 0＜a＜时满足要求．综上可知 a∈.(2)由题意知，0≤x－1≤1，解得 2≤x≤4.因此，函数 f 的定义域为[2,4]．]求函数定义域的类型与方法1 已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值范围.2 实际问题：求函数的定义域既要考虑解析式有意义，还应考虑使实际问题有意义.3 复合函数问题：① 若 fx的定义域为[a，b]，fgx的定义域应由 a≤gx≤b 解出；② 若 fgx的定义域为[a，b]，则 fx的定义域为 gx在[a，b]上的值域.,注意：① fx中的 x与 fgx中的 gx地位相同；②定义域所指永远是 x 的范围.1．已知函数 f(2x－1)的定义域为[0,1)，求 f(1－3x)的定义域．[解] 由 0≤x<1，得－1≤2x－1<1，所以，f(x)的定义域是[－1,1)．由－1≤1－3x<1，得 00，则 x 的取值范围是________．(2)函数 y＝|2x－1|的单调递增区间是________．[思路探究] (1)将原不等式化为 f(x－1)>f(2)，再利用函数的单调性将其转化为 x－1<2 来解；(2)画出函数的图像求解．(1)x<3 (2) [(1) f(2)＝0，∴不等式 f(x－1)>0，即为 f(x－1)>f(2)，又 f(x)是 R 上的减函数，则 x－1<2，解得 x<3.(2)函数 y＝|2x－1|的图像如下：由图像知，其单调递增区间是.]1 fx是 A 上的增函数⇔对任意 x1，x2∈A，当 x1≠x2时，\f(fx2－fx1,x2－x1)>0，fx是 A 上的减函数⇔对任意 x1，x2∈A，当 x1≠x2时，.2 若 fx是单调递增减函数，则①fx2> fx1⇔x2>x1x2x1.2．(1)已知 f(x)＝x，若 0