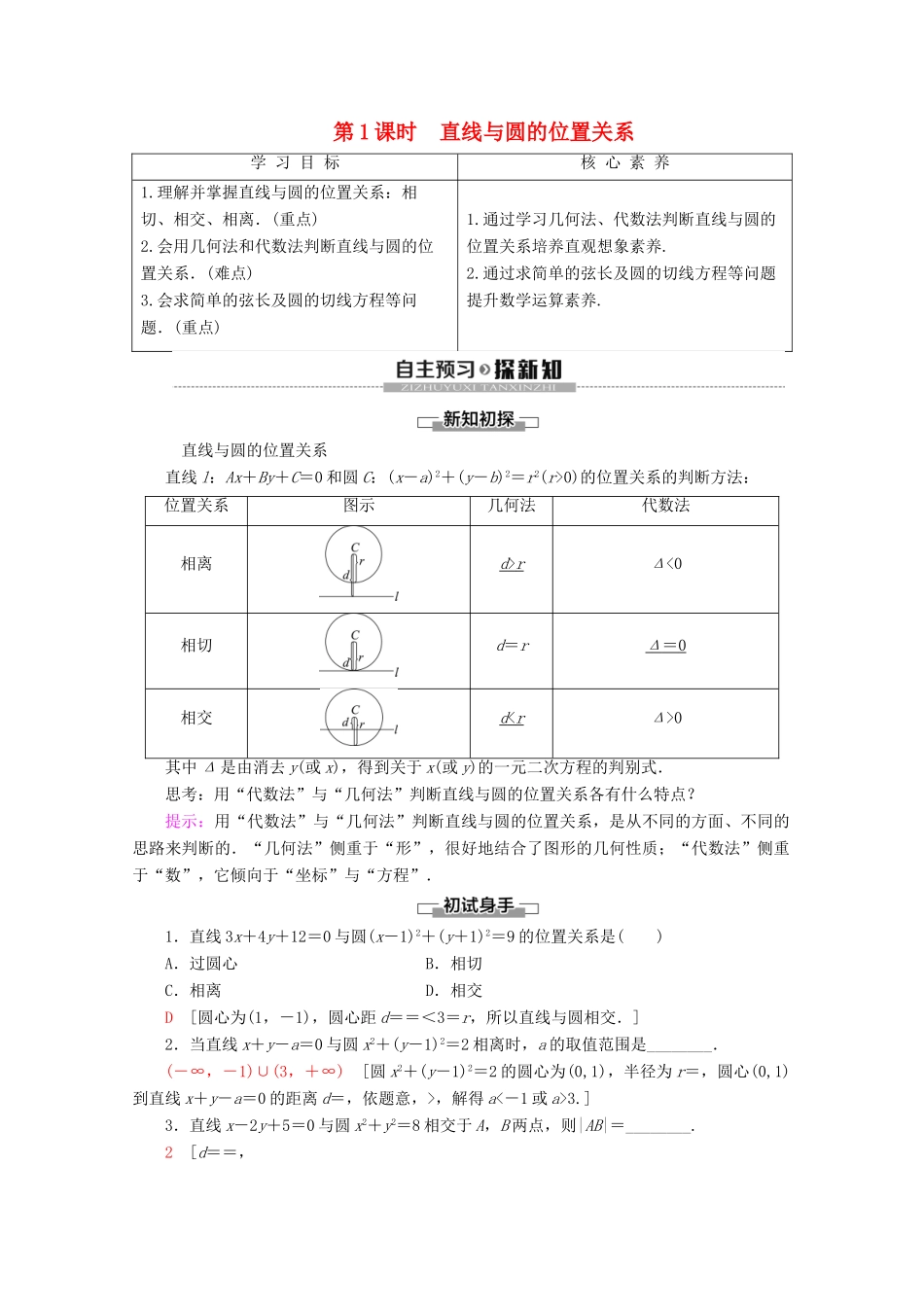
第 1 课时 直线与圆的位置关系学 习 目 标核 心 素 养1.理解并掌握直线与圆的位置关系:相切、相交、相离.(重点)2.会用几何法和代数法判断直线与圆的位置关系.(难点)3.会求简单的弦长及圆的切线方程等问题.(重点)1.通过学习几何法、代数法判断直线与圆的位置关系培养直观想象素养.2.通过求简单的弦长及圆的切线方程等问题提升数学运算素养. 直线与圆的位置关系直线 l:Ax+By+C=0 和圆 C:(x-a)2+(y-b)2=r2(r>0)的位置关系的判断方法:位置关系图示几何法代数法相离d > r Δ<0相切d=rΔ = 0 相交d < r Δ>0其中 Δ 是由消去 y(或 x),得到关于 x(或 y)的一元二次方程的判别式.思考:用“代数法”与“几何法”判断直线与圆的位置关系各有什么特点?提示:用“代数法”与“几何法”判断直线与圆的位置关系,是从不同的方面、不同的思路来判断的.“几何法”侧重于“形”,很好地结合了图形的几何性质;“代数法”侧重于“数”,它倾向于“坐标”与“方程”.1.直线 3x+4y+12=0 与圆(x-1)2+(y+1)2=9 的位置关系是( )A.过圆心 B.相切C.相离 D.相交D [圆心为(1,-1),圆心距 d==<3=r,所以直线与圆相交.]2.当直线 x+y-a=0 与圆 x2+(y-1)2=2 相离时,a 的取值范围是________.(-∞,-1)∪(3,+∞) [圆 x2+(y-1)2=2 的圆心为(0,1),半径为 r=,圆心(0,1)到直线 x+y-a=0 的距离 d=,依题意,>,解得 a<-1 或 a>3.]3.直线 x-2y+5=0 与圆 x2+y2=8 相交于 A,B 两点,则|AB|=________.2 [d==,所以|AB|=2=2=2.]直线与圆位置关系的判断【例 1】 已知直线方程 mx-y-m-1=0,圆的方程 x2+y2-4x-2y+1=0.当 m 为何值时,圆与直线:有两个公共点;只有一个公共点;没有公共点.[解] 法一:将直线 mx-y-m-1=0 代入圆的方程化简整理得,(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0. Δ=4m(3m+4),∴当 Δ>0 时,即 m>0 或 m<-时,直线与圆相交,即直线与圆有两个公共点;当 Δ=0 时,即 m=0 或 m=-时,直线与圆相切,即直线与圆只有一个公共点;当 Δ<0 时,即-0 或 m<-时,直线与圆相交,即直线...