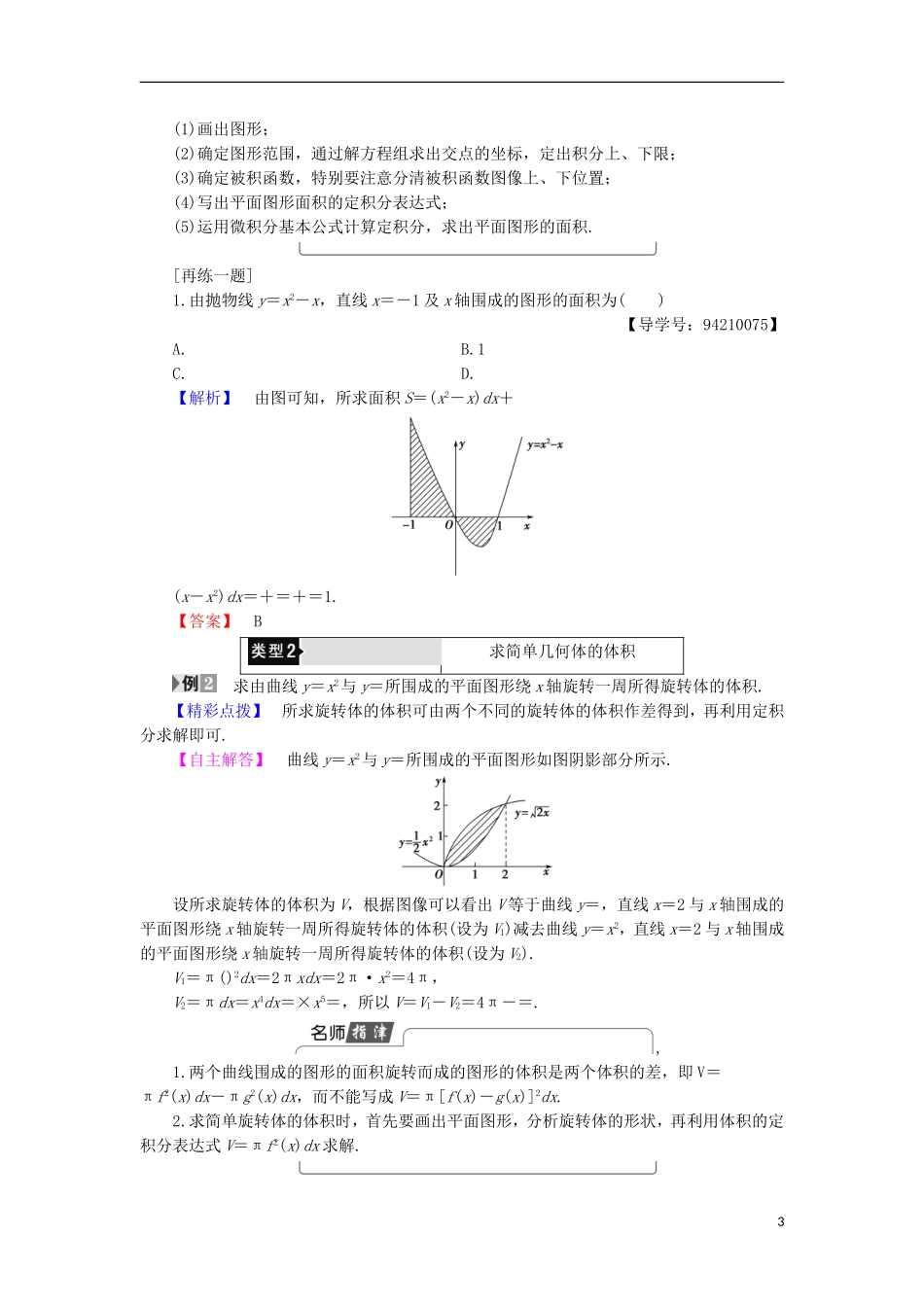
§3 定积分的简单应用1.会用定积分求平面图形的面积.(重点)2.会用定积分求简单几何体的体积.(重点)3.理解建立实际问题的积分模型的基本过程和方法.(难点)[基础·初探]教材整理 1 平面图形的面积阅读教材 P87~P88“例 3”以上部分,完成下列问题.1.当 x∈[a,b]时,若 f(x)>0,由直线 x=a,x=b(a≠b),y=0 和曲线 y=f(x)所围成的曲边梯形的面积 S=f ( x ) dx .2.当 x∈[a,b]时,若 f(x)<0,由直线 x=a,x=b(a≠b),y=0 和曲线 y=f(x)围成的曲边梯形的面积 S=- f ( x ) dx .图 4313.当 x∈[a,b]时,若 f(x)>g(x)>0,由直线 x=a,x=b(a≠b)和曲线 y=f(x),y=g(x)围成的平面图形的面积 S=[ f ( x ) - g ( x )] dx .(如图 431)判断(正确的打“√”,错误的打“×”)(1)曲线 y=sin x,x∈与 x 轴围成的图形的面积为 sin xdx.( )(2)曲线 y=x3与直线 x+y=2,y=0 围成的图形的面积为 x3dx+(2-x)dx.( )(3)曲线 y=3-x2与直线 y=-1 围成的图形的面积为(4-x2)dx.( )【答案】 (1)× (2)√ (3)√教材整理 2 简单旋转几何体的体积阅读教材 P89~P90“练习”以上部分,完成下列问题.旋转体可看作由连续曲线 y=f(x),直线 x=a,x=b 及 x 轴所围成的曲边梯形绕 x 轴旋转一周而成的几何体,该几何体的体积为 V = π[ f ( x )] 2 dx .由 y=x2,x=1 和 y=0 所围成的平面图形绕 x 轴旋转所得的旋转体的体积为( )A.B.C.D.【解析】 V=πy2dx=π(x2)2dx=x5=.【答案】 C1[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问 1: 解惑: 疑问 2: 解惑: 疑问 3: 解惑: [小组合作型]利用定积分求平面图形的面积 (1)求由直线 y=x+3,曲线 y=x2-6x+13 所围图形的面积 S;(2)求由曲线 y=x2,直线 y=2x 和 y=x 围成的图形的面积.【精彩点拨】 (1)作出两函数的图像,并求其交点坐标.确定积分区间,利用定积分求面积 S.(2)求出三条曲线的不同的交点横坐标,将积分区间细化,分别求出相应区间曲边梯形的面积再求和,注意在每个区间上被积函数均是由上减下.【自主解答】 (1)作出直线 y=x+3,曲线 y=x2-6x+13 的草图,所求面积为图中阴影部分的面积.解方程组得交点坐标为(2,5)和(5,8).因此,所求图形的面积 S=(x+3)dx-(x2-6x+13)dx=(-x2+7x-10)dx==.(2)法一...