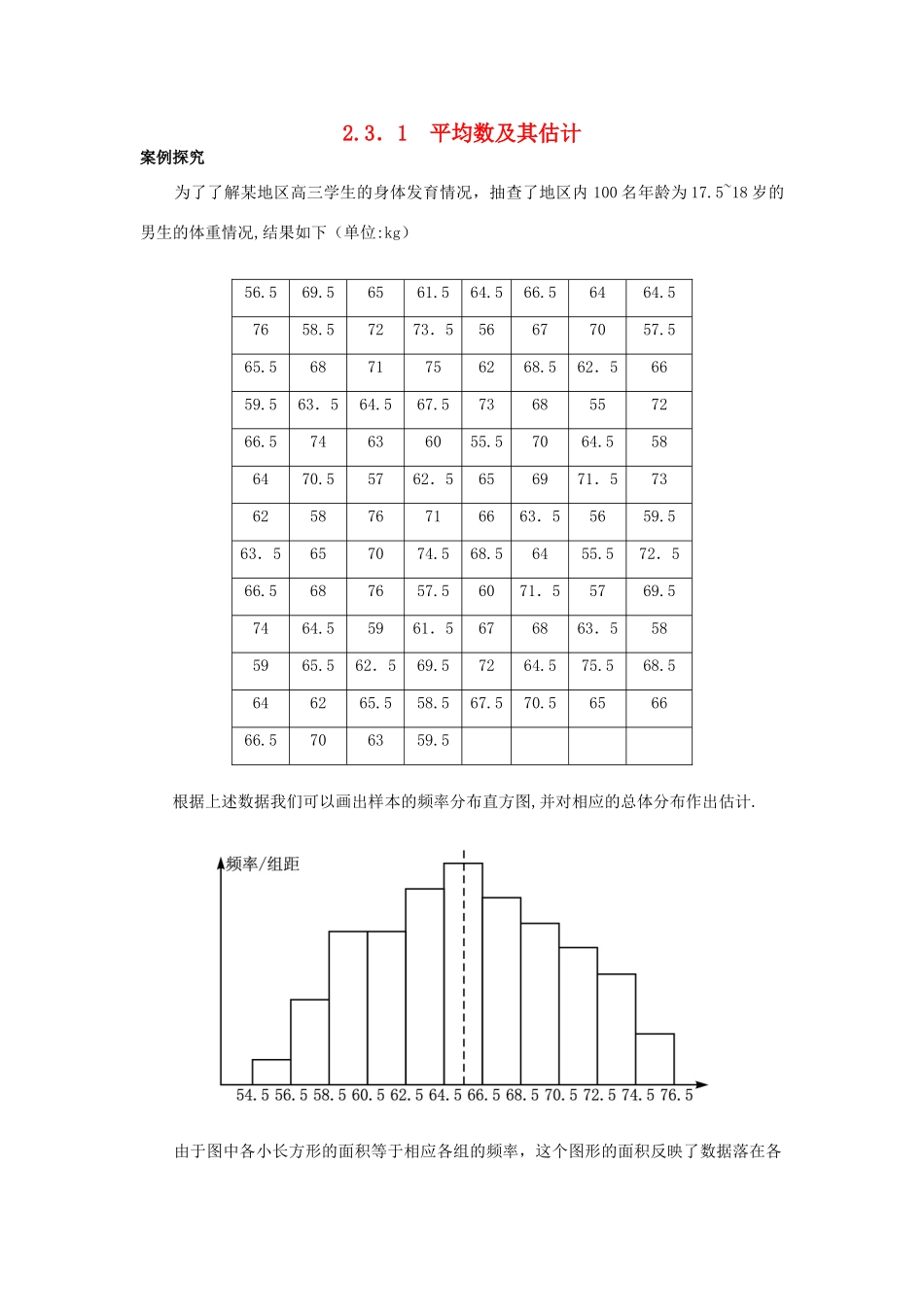
2.3.1 平均数及其估计案例探究 为了了解某地区高三学生的身体发育情况,抽查了地区内 100 名年龄为 17.5~18 岁的男生的体重情况,结果如下(单位:kg)56.569.56561.564.566.56464.57658.57273.556677057.565.56871756268.562.56659.563.564.567.57368557266.574636055.57064.5586470.55762.5656971.573625876716663.55659.563.5657074.568.56455.572.566.5687657.56071.55769.57464.55961.5676863.5585965.562.569.57264.575.568.5646265.558.567.570.5656666.5706359.5根据上述数据我们可以画出样本的频率分布直方图,并对相应的总体分布作出估计. 由于图中各小长方形的面积等于相应各组的频率,这个图形的面积反映了数据落在各个小组的频率的大小.在得到了样本的频率后,就可以对相应的总体情况作出估计.例如从这些样本数据的频率分布直方图可以看出,体重在(64.5,66.5)kg 的学生比体重为其他值的学生数多,但他并没有告诉我们多多少. 试问:怎样将各个样本数据汇总为一个数值,并使它成为样本数据的“中心点”? 能否用一个数值来描写样本数据的离散程度? 初中我们曾经学过众数、中位数、平均数等各种数字特征.应当说,这些数字都能够为我们提供关于样本数据的特征信息. 我们常用算术平均数(其中 ai(i=1,2,…,n)为 n 个实验数据)作为体重的最理想的近似值,它的依据是什么呢? 处理实验数据的原则是使这个近似值与实验数据之间的离差最小,设这个近似值为x,那么它与 n 个实验值 ai(i=1,2,…,n)的离差分别为x-a1,x-a2,x-a3,…,x-an.由于上述离差有正有负,故不宜直接相加.可以考虑将各个离差的绝对值相加,研究|x-a1|+|x-a2|+…+|x-an|取最小值时 x 的值.但由于含有绝对值,运算不太方便,所以,考虑离差的平方和,即 (x-a1)2+(x-a2)2+…+(x-an)2, 当此和最小时,对应的 x 的值作为近似值.因为 (x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+a12+a22+…+an2, 所以当 x=时离差的平方和最小,故可用作为表示体重的理想近似值,称其为这 n 个数据 a1,a2,…,an 的平均数(average)或均值(mean),一般记为=. 这样,我们可以用计算器求得,该地区内 100 名年龄为 17.5~18 岁的男生的体重的最佳近似值为 x=65.5(kg). 这样我们就得到了样本平均数的求解方法: 样本数据的算术平均数,即=.Excel 中 函 数 “ AVERAGE ( ) ”...