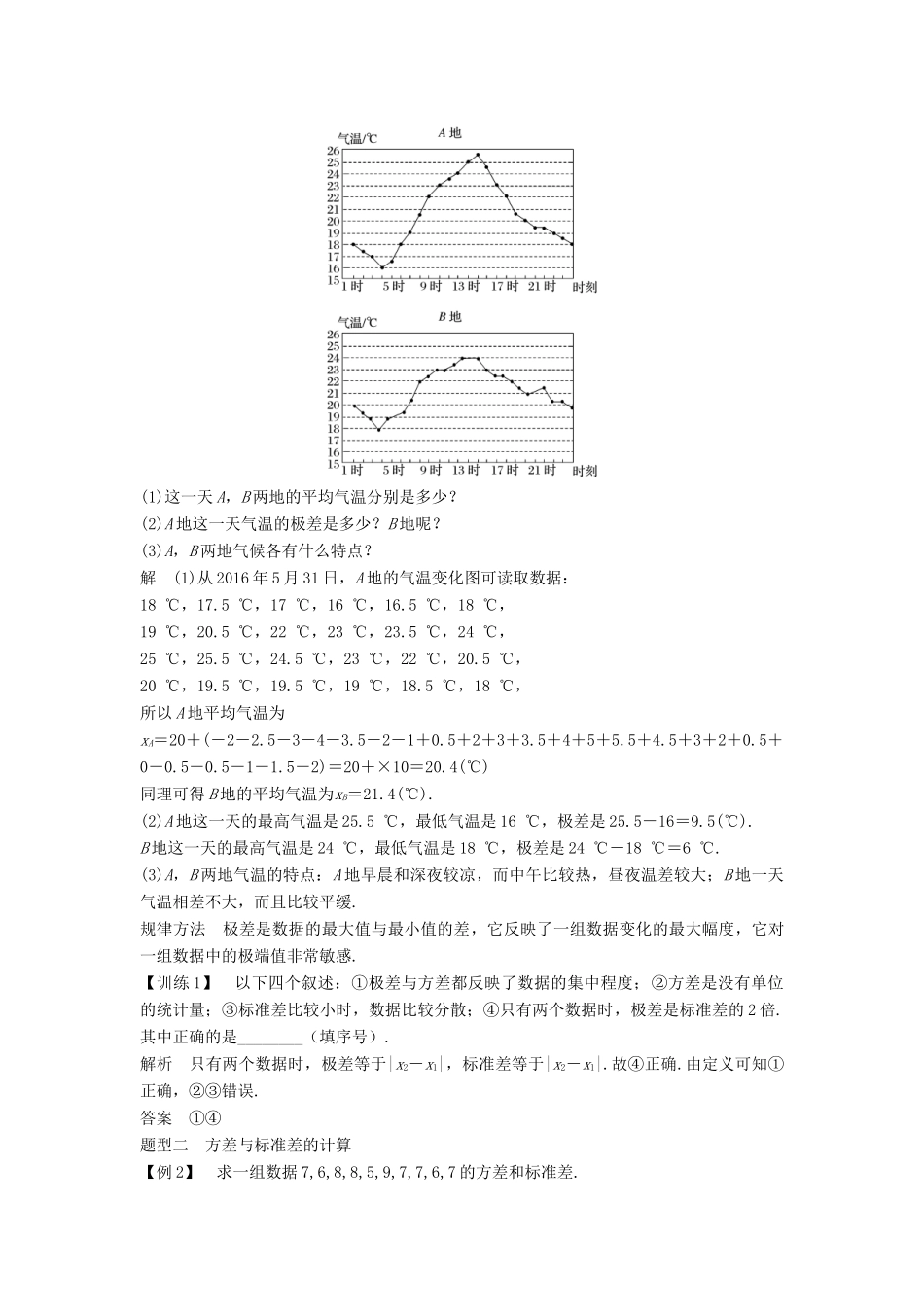
2.3.2 方差与标准差内容要求 1.会求样本标准差、方差(重点);2.理解用样本的数字特征来估计总体数字特征的方法(难点);3.会应用相关知识解决简单的统计实际问题.(重点)知识点一 标准差、方差、极差1.极差一组数据的最大值与最小值的差称为极差.2.标准差(1)平均距离与标准差标准差是样本数据到平均数的一种平均距离,一般用 s 表示.假设样本数据是 x1,x2,…,xn,x表示这组数据的平均数.xi 到x的距离是|xi-x|(i=1,2,…,n),则用如下公式来计算标准差:s= (2)计算标准差的步骤① 求样本数据的平均数x;② 求每个样本数据与样本平均数的差 xi-x (i=1,2,…,n);③ 求(xi-x)2(i=1,2,…,n);④ 求 s2=[(x1-x)2+(x2-x)2+…+(xn-x)2];⑤ 求 s=,即为标准差.3.方差标准差的平方 s2叫做方差.s2=[(x1-x)2+(x2-x)2+…+(xn-x)2],其中,xi(i=1,2,…,n)是样本数据,n 是样本容量,x是样本平均数 . 【预习评价】 (正确的打“√”,错误的打“×”)1.方差越小,表示波动越大,越不稳定.( )2.求平均数是求方差、标准差的前提.( )3.平均数反映了总体的平均水平.( )答案 1.× 2.√ 3.√题型一 极差【例 1】 2016 年 5 月 31 日 A,B 两地的气温变化如图所示.(1)这一天 A,B 两地的平均气温分别是多少?(2)A 地这一天气温的极差是多少?B 地呢?(3)A,B 两地气候各有什么特点?解 (1)从 2016 年 5 月 31 日,A 地的气温变化图可读取数据:18 ℃,17.5 ℃,17 ℃,16 ℃,16.5 ℃,18 ℃,19 ℃,20.5 ℃,22 ℃,23 ℃,23.5 ℃,24 ℃,25 ℃,25.5 ℃,24.5 ℃,23 ℃,22 ℃,20.5 ℃,20 ℃,19.5 ℃,19.5 ℃,19 ℃,18.5 ℃,18 ℃,所以 A 地平均气温为xA=20+(-2-2.5-3-4-3.5-2-1+0.5+2+3+3.5+4+5+5.5+4.5+3+2+0.5+0-0.5-0.5-1-1.5-2)=20+×10=20.4(℃)同理可得 B 地的平均气温为xB=21.4(℃).(2)A 地这一天的最高气温是 25.5 ℃,最低气温是 16 ℃,极差是 25.5-16=9.5(℃).B 地这一天的最高气温是 24 ℃,最低气温是 18 ℃,极差是 24 ℃-18 ℃=6 ℃.(3)A,B 两地气温的特点:A 地早晨和深夜较凉,而中午比较热,昼夜温差较大;B 地一天气温相差不大,而且比较平缓.规律方法 极差是数据的最大值与最小值的差,它反映了一组数据变化的最大幅度,它对一组数据中的极端值非常敏感.【训...