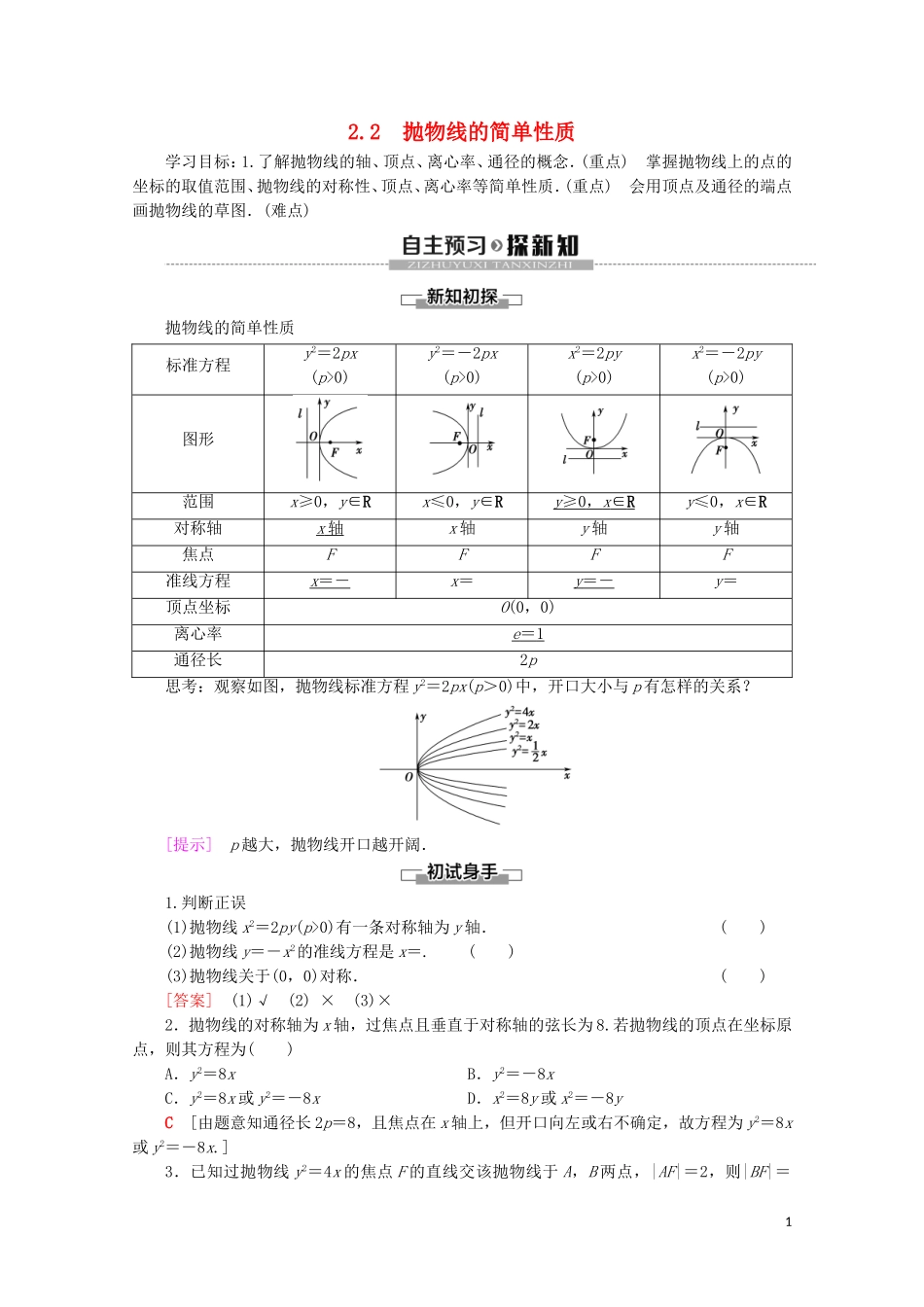
2.2 抛物线的简单性质学习目标:1.了解抛物线的轴、顶点、离心率、通径的概念.(重点) 掌握抛物线上的点的坐标的取值范围、抛物线的对称性、顶点、离心率等简单性质.(重点) 会用顶点及通径的端点画抛物线的草图.(难点)抛物线的简单性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形范围x≥0,y∈Rx≤0,y∈Ry ≥0 , x ∈ R y≤0,x∈R对称轴x 轴 x 轴y 轴y 轴焦点FFFF准线方程x =- x=y =- y=顶点坐标O(0,0)离心率e = 1 通径长2p思考:观察如图,抛物线标准方程 y2=2px(p>0)中,开口大小与 p 有怎样的关系?[提示] p 越大,抛物线开口越开阔.1.判断正误(1)抛物线 x2=2py(p>0)有一条对称轴为 y 轴.( )(2)抛物线 y=-x2的准线方程是 x=.( )(3)抛物线关于(0,0)对称.( )[答案] (1)√ (2) × (3)×2.拋物线的对称轴为 x 轴,过焦点且垂直于对称轴的弦长为 8.若拋物线的顶点在坐标原点,则其方程为( )A.y2=8x B.y2=-8xC.y2=8x 或 y2=-8x D.x2=8y 或 x2=-8yC [由题意知通径长 2p=8,且焦点在 x 轴上,但开口向左或右不确定,故方程为 y2=8x或 y2=-8x.]3.已知过抛物线 y2=4x 的焦点 F 的直线交该抛物线于 A,B 两点,|AF|=2,则|BF|=1________.2 [F(1,0),由抛物线定义得 A 点横坐标为 1.∴AF⊥x 轴,∴|BF|=|AF|=2.]4.顶点在原点,对称轴是 x 轴,并且顶点与焦点的距离等于 6 的抛物线方程是________.y2=24x 或 y2=-24x [ 顶点与焦点距离为 6,即=6,∴2p=24,又 对称轴为 x 轴,∴抛物线方程为 y2=24x 或 y2=-24x.]抛物线的几何性质【例 1】 正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线 y2=2px(p>0)上,求这个正三角形的边长.[解] 如图,设正三角形 OAB 的顶点 A,B 在抛物线上,且它们坐标分别为(x1,y1)和(x2,y2)则:y=2px1,y=2px2.又|OA|=|OB|,∴x+y=x+y,即 x-x+2px1-2px2=0,∴(x1-x2)(x1+x2+2p)=0. x1>0,x2>0,2p>0,∴x1=x2,由此可得|y1|=|y2|,即线段 AB 关于 x 轴对称.由于 AB 垂直于 x 轴,且∠AOx=30°.∴=tan 30°=,而 y=2px1,∴y1=2p.于是|AB|=2y1=4p.1.注意抛物线各元素间的关系:抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线的准线与对...