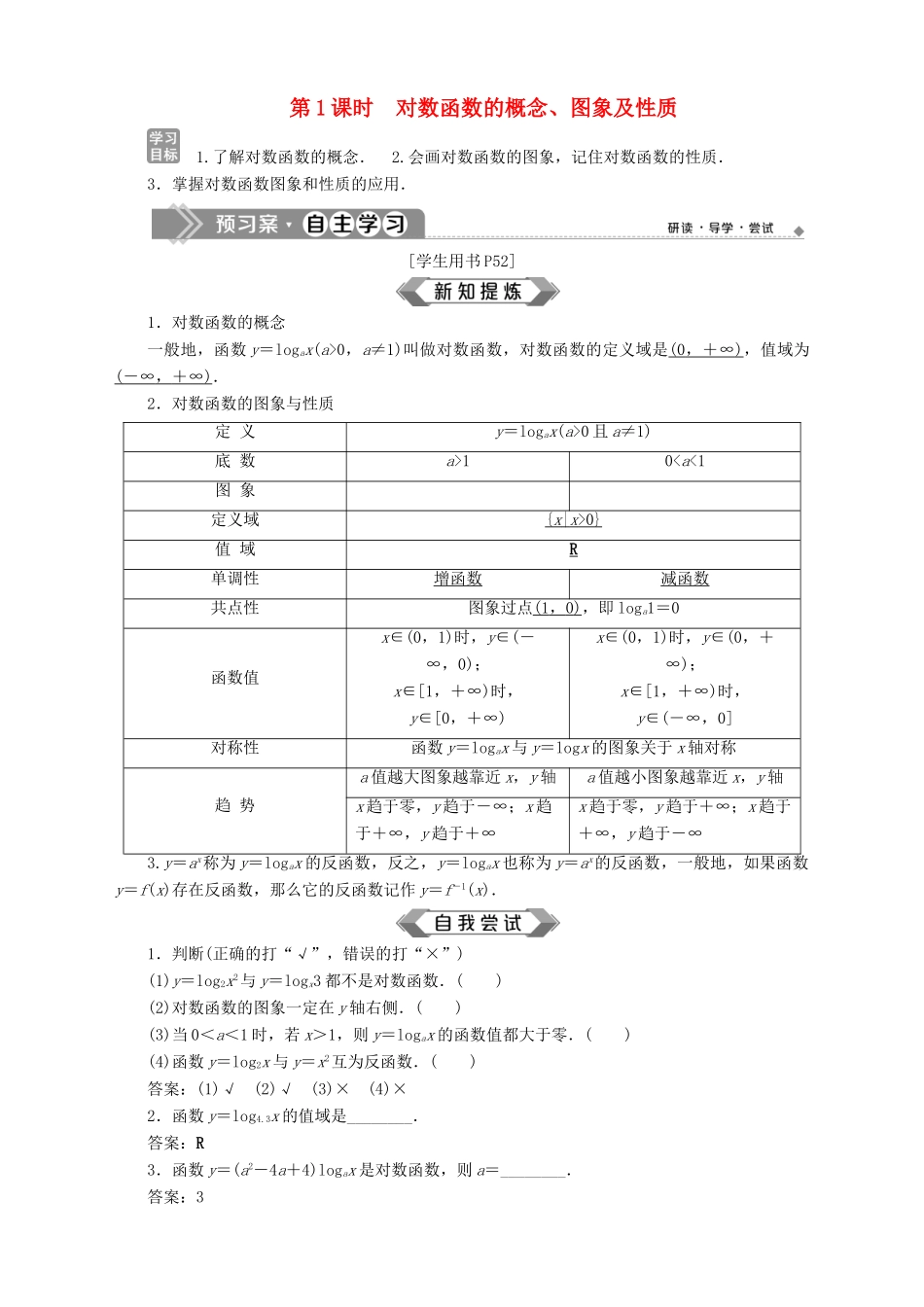
第 1 课时 对数函数的概念、图象及性质 1.了解对数函数的概念. 2.会画对数函数的图象,记住对数函数的性质.3.掌握对数函数图象和性质的应用. [学生用书 P52]1.对数函数的概念一般地,函数 y=logax(a>0,a≠1)叫做对数函数,对数函数的定义域是(0 ,+∞ ) ,值域为( -∞ , +∞ ) .2.对数函数的图象与性质定 义y=logax(a>0 且 a≠1)底 数a>10
0} 值 域R单调性增函数减函数共点性图象过点(1 , 0 ) ,即 loga1=0函数值x∈(0,1)时,y∈(-∞,0);x∈[1,+∞)时,y∈[0,+∞)x∈(0,1)时,y∈(0,+∞);x∈[1,+∞)时,y∈(-∞,0]对称性函数 y=logax 与 y=logx 的图象关于 x 轴对称趋 势a 值越大图象越靠近 x,y 轴a 值越小图象越靠近 x,y 轴x 趋于零,y 趋于-∞;x 趋于+∞,y 趋于+∞x 趋于零,y 趋于+∞;x 趋于+∞,y 趋于-∞3.y=ax称为 y=logax 的反函数,反之,y=logax 也称为 y=ax的反函数,一般地,如果函数y=f(x)存在反函数,那么它的反函数记作 y=f-1(x).1.判断(正确的打“√”,错误的打“×”)(1)y=log2x2与 y=logx3 都不是对数函数.( )(2)对数函数的图象一定在 y 轴右侧.( )(3)当 0<a<1 时,若 x>1,则 y=logax 的函数值都大于零.( )(4)函数 y=log2x 与 y=x2互为反函数.( )答案:(1)√ (2)√ (3)× (4)×2.函数 y=log4.3x 的值域是________.答案:R3.函数 y=(a2-4a+4)logax 是对数函数,则 a=________.答案:34.函数 f(x)=log5(1-x)的定义域是________.答案:{x|x<1} 与对数函数有关的定义域问题[学生用书 P52] 求下列函数的定义域:(1)y=lg(x+1)+;(2)y=log(2x-1).【解】 (1)要使函数有意义,需即所以-1<x<1.所以函数的定义域为(-1,1).(2)由解得 x>,且 x≠1,所以函数的定义域为∪(1,+∞). 若将例题(2)函数改为“y=log(2x-1)”,则其定义域应为________.解析:由解得 x>,且 x≠1,所以函数的定义域为∪(1,+∞).答案:∪(1,+∞)(1)求与对数函数有关的函数定义域时应遵循的原则① 分母不能为 0;② 根指数为偶数时,被开方数非负;③ 对数的真数大于 0,底数大于 0 且不为 1.(2)求函数定义域的步骤① 列出使函数有意义的不等式(组);② 化简并解出自变量的取值范围;③ 确定函数的定义域. 1.求下列函数的定...