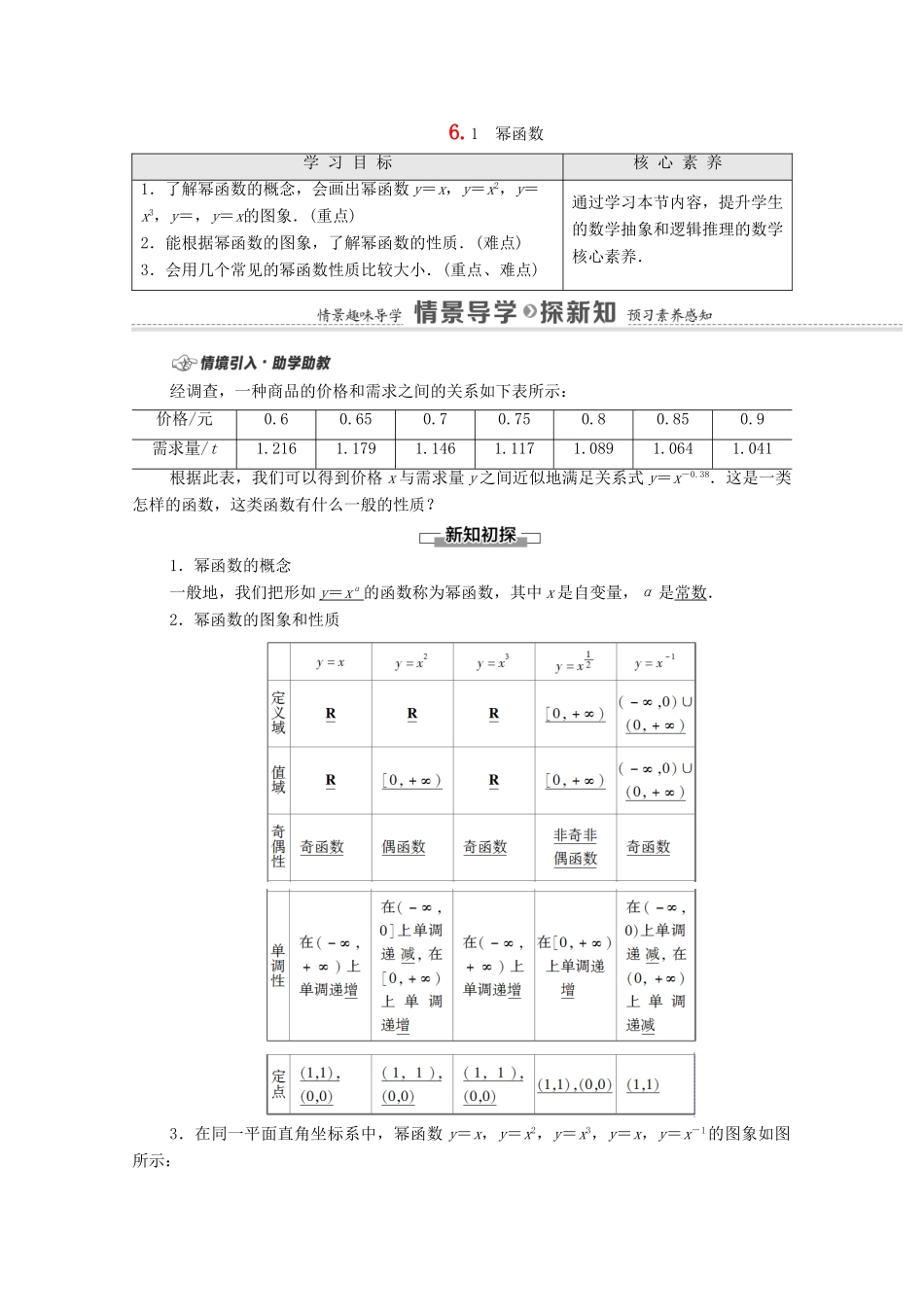
6.1 幂函数学 习 目 标核 心 素 养1.了解幂函数的概念,会画出幂函数 y=x,y=x2,y=x3,y=,y=x的图象.(重点)2.能根据幂函数的图象,了解幂函数的性质.(难点)3.会用几个常见的幂函数性质比较大小.(重点、难点)通过学习本节内容,提升学生的数学抽象和逻辑推理的数学核心素养.经调查,一种商品的价格和需求之间的关系如下表所示:价格/元0.60.650.70.750.80.850.9需求量/t1.2161.1791.1461.1171.0891.0641.041根据此表,我们可以得到价格 x 与需求量 y 之间近似地满足关系式 y=x-0.38.这是一类怎样的函数,这类函数有什么一般的性质?1.幂函数的概念一般地,我们把形如 y = x α 的函数称为幂函数,其中 x 是自变量,α 是常数.2.幂函数的图象和性质3.在同一平面直角坐标系中,幂函数 y=x,y=x2,y=x3,y=x,y=x-1的图象如图所示:1.思考辨析(正确的打“√”,错误的打“×”)(1)幂函数的图象不经过第四象限.( )(2)幂函数的图象必过(0,0)和(1,1)这两点.( )(3)幂函数 y=xα的定义域为 R,与指数也无关.( )[提示] (1)由幂函数的一般式 y=xα(α 为常数)及图象可知,当 x>0 时,y>0,即图象不经过第四象限.(2)y=x-1不经过(0,0)点,故错误.(3)y=x,定义域为[0,+∞),与指数有关,故错误.[答案] (1)√ (2)× (3)×2.若 y=mxα+(2n-4)是幂函数,则 m+n= .3 [由题意得所以 m+n=3.]3.已知幂函数 f(x)=xα的图象经过点(2,8),则 f(-2)= .-8 [8=2α,所以 α=3,所以 f(x)=x3,f(-2)=(-2)3=-8.]幂函数的概念【例 1】 已知 y=(m2+2m-2)x+2n-3 是幂函数,求 m,n 的值.[思路点拨] 由幂函数的定义列式求解.[解] 由题意得解得∴m=-3,n=为所求.1.幂函数 y=xα满足的三个特征(1)幂 xα前系数为 1;(2)底数只能是自变量 x,指数是常数;(3)项数只有一项.2.求幂函数解析式时常用待定系数法,即设解析式为 f(x)=xα,根据条件求出 α.[跟进训练]1.下列函数是幂函数的有 .(填序号)①y=x2x;② y=2x2;③ y=;④ y=x2+1;⑤ y=-;⑥ y=x.③⑥ [根据幂函数的定义,只有③⑥符合题意.]2.已知幂函数 f(x)=xα的图象经过,则 f(100)= . [由题知 2α==2,∴α=-.∴f(x)=x,∴f(100)=100==.]比较大小【例 2】 比较下列各组数中两个数的大小:(1)与;(2)与;(3)0.25与 6.25;(4)1.2...