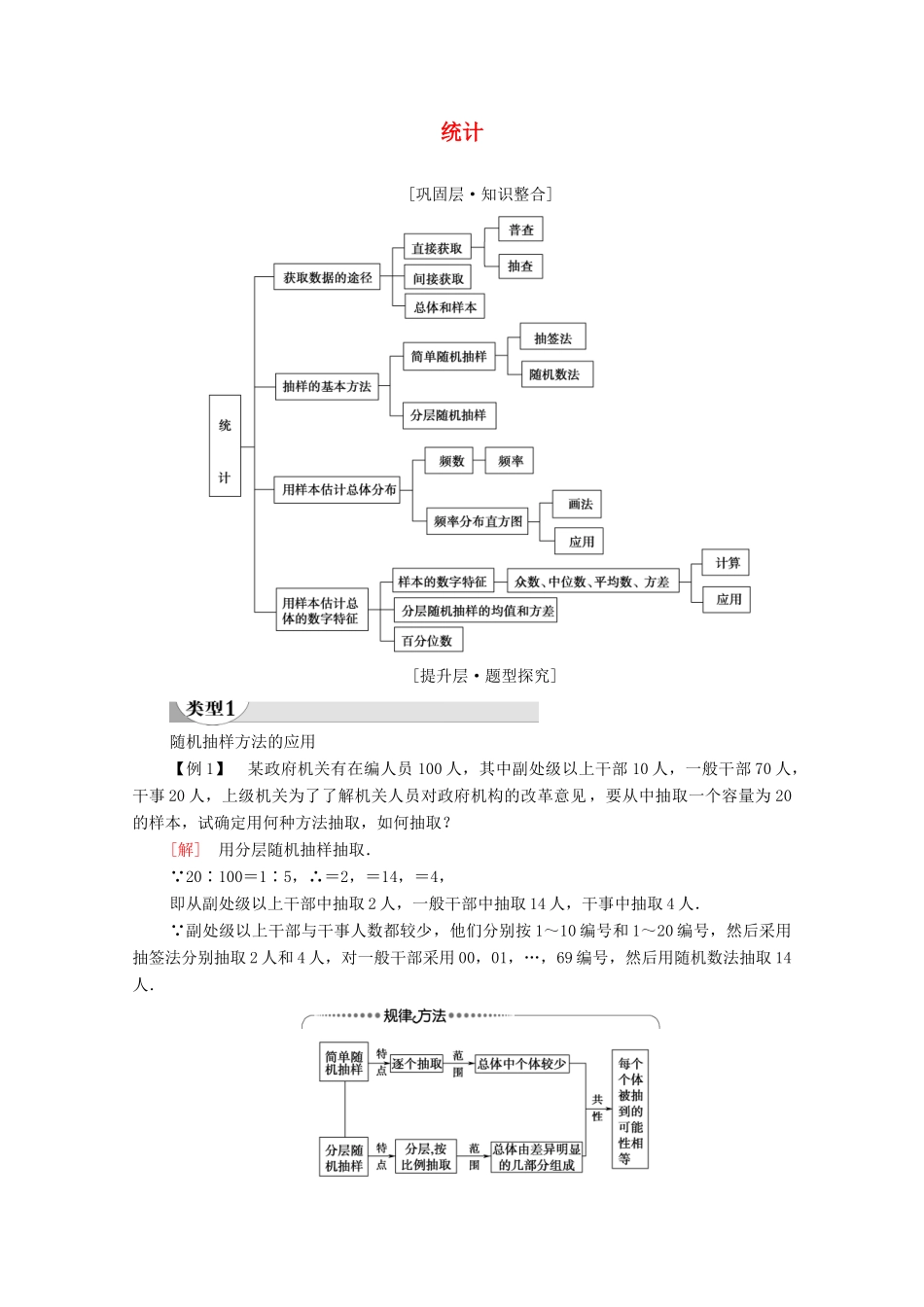
统计[巩固层·知识整合] [提升层·题型探究]随机抽样方法的应用【例 1】 某政府机关有在编人员 100 人,其中副处级以上干部 10 人,一般干部 70 人,干事 20 人,上级机关为了了解机关人员对政府机构的改革意见,要从中抽取一个容量为 20的样本,试确定用何种方法抽取,如何抽取?[解] 用分层随机抽样抽取. 20∶100=1∶5,∴=2,=14,=4,即从副处级以上干部中抽取 2 人,一般干部中抽取 14 人,干事中抽取 4 人. 副处级以上干部与干事人数都较少,他们分别按 1~10 编号和 1~20 编号,然后采用抽签法分别抽取 2 人和 4 人,对一般干部采用 00,01,…,69 编号,然后用随机数法抽取 14人. 1.某学校有教师 200 人,男学生 1 200 人,女学生 1 000 人.现用分层随机抽样的方法从全体师生中抽取一个容量为 n 的样本,若女学生一共抽取了 80 人,则 n 的值为( )A.193 B.192 C.191 D.190B [1 000×=80,求得 n=192.]用样本估计总体【例 2】 某花木公司为了调查某种树苗的生长情况,抽取了一个容量为 100 的样本,测得树苗的高度(cm)数据的分组及相应频数如下:[107,109)3 株;[109,111)9 株;[111,113)13 株;[113,115)16 株;[115,117)26 株;[117,119)20 株;[119,121)7 株;[121,123)4 株;[123,125]2 株.(1)列出频率分布表;(2)画出频率分布直方图;(3)据上述图表,估计数据在[109,121)范围内的可能性是百分之几?[解] 分组频数频率累积频率[107,109)30.030.03[109,111)90.090.12[111,113)130.130.25[113,115)160.160.41[115,117)260.260.67[117,119)200.200.87[119,121)70.070.94[121,123)40.040.98[123,125]20.021.00合计1001.00(2)频率分布直方图如下: (3)由上述图表可知数据落在[109,121)范围内的频率为:0.94-0.03=0.91,即数据落在[109,121)范围内的可能性是 91%.1.在本例中由得到的频率分布直方图估计树苗的高度(cm)的众数和中位数.[解] 众数是频率分布直方图中最高小矩形的底边的中点,即估计众数为 116,因为前 4 组数据的累计频率是 0.41,前 5 组数据的累计频率是 0.67,所以中位数在[115,117)内,设中位数为 x,则 0.41+2(x-115)=0.5,解得 x=115.045,即中位数的估计值为 115.045.2.在本例中由得到的频率分布直方图估计树苗的高度(cm)的平均数.[解] 由频率分布直方图可得树苗的高度(cm)的平均...