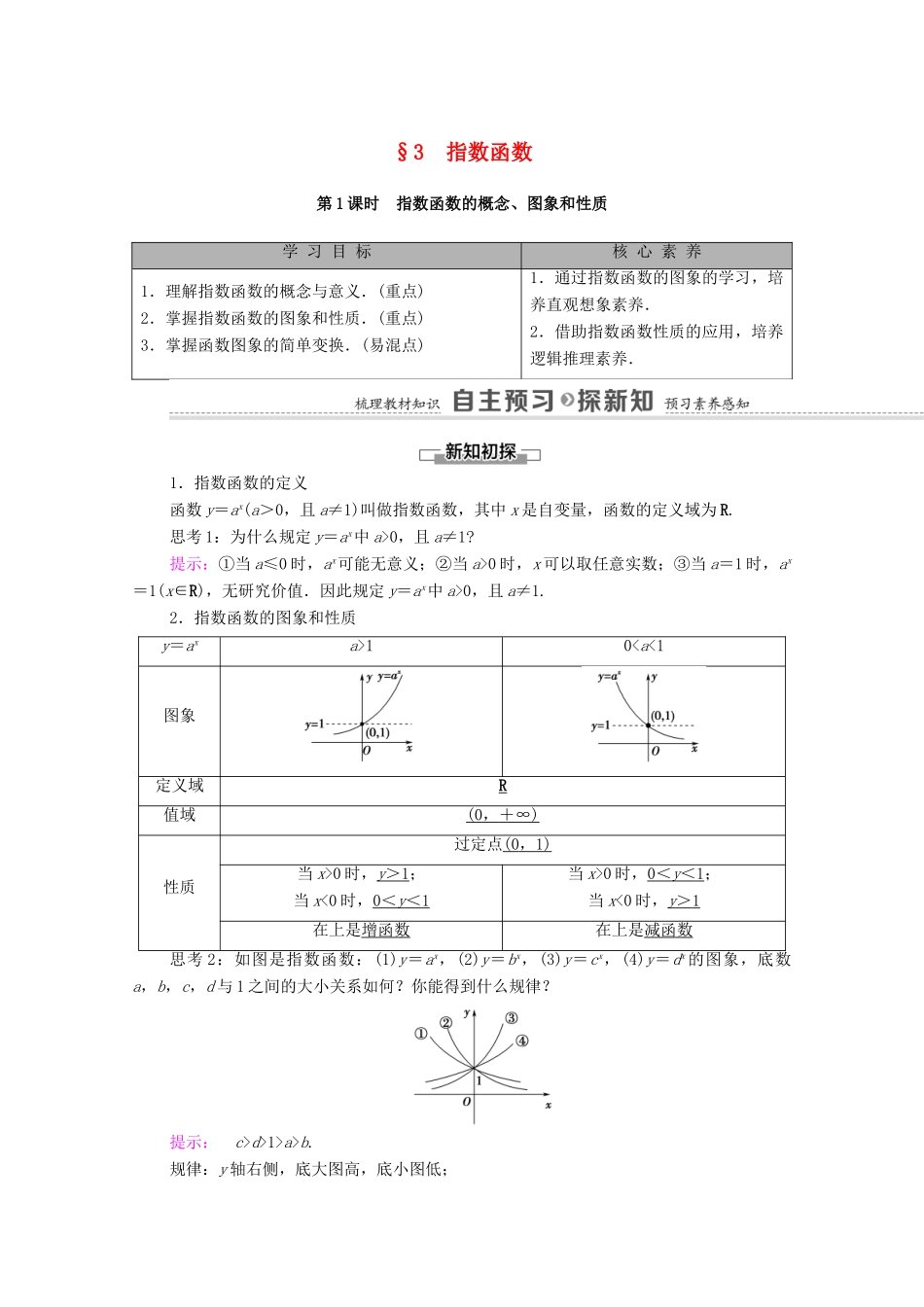
§3 指数函数第 1 课时 指数函数的概念、图象和性质学 习 目 标核 心 素 养1.理解指数函数的概念与意义.(重点)2.掌握指数函数的图象和性质.(重点)3.掌握函数图象的简单变换.(易混点)1.通过指数函数的图象的学习,培养直观想象素养.2.借助指数函数性质的应用,培养逻辑推理素养.1.指数函数的定义函数 y=ax(a>0,且 a≠1)叫做指数函数,其中 x 是自变量,函数的定义域为 R.思考 1:为什么规定 y=ax中 a>0,且 a≠1?提示:①当 a≤0 时,ax可能无意义;②当 a>0 时,x 可以取任意实数;③当 a=1 时,ax=1(x∈R),无研究价值.因此规定 y=ax中 a>0,且 a≠1.2.指数函数的图象和性质y=axa>10
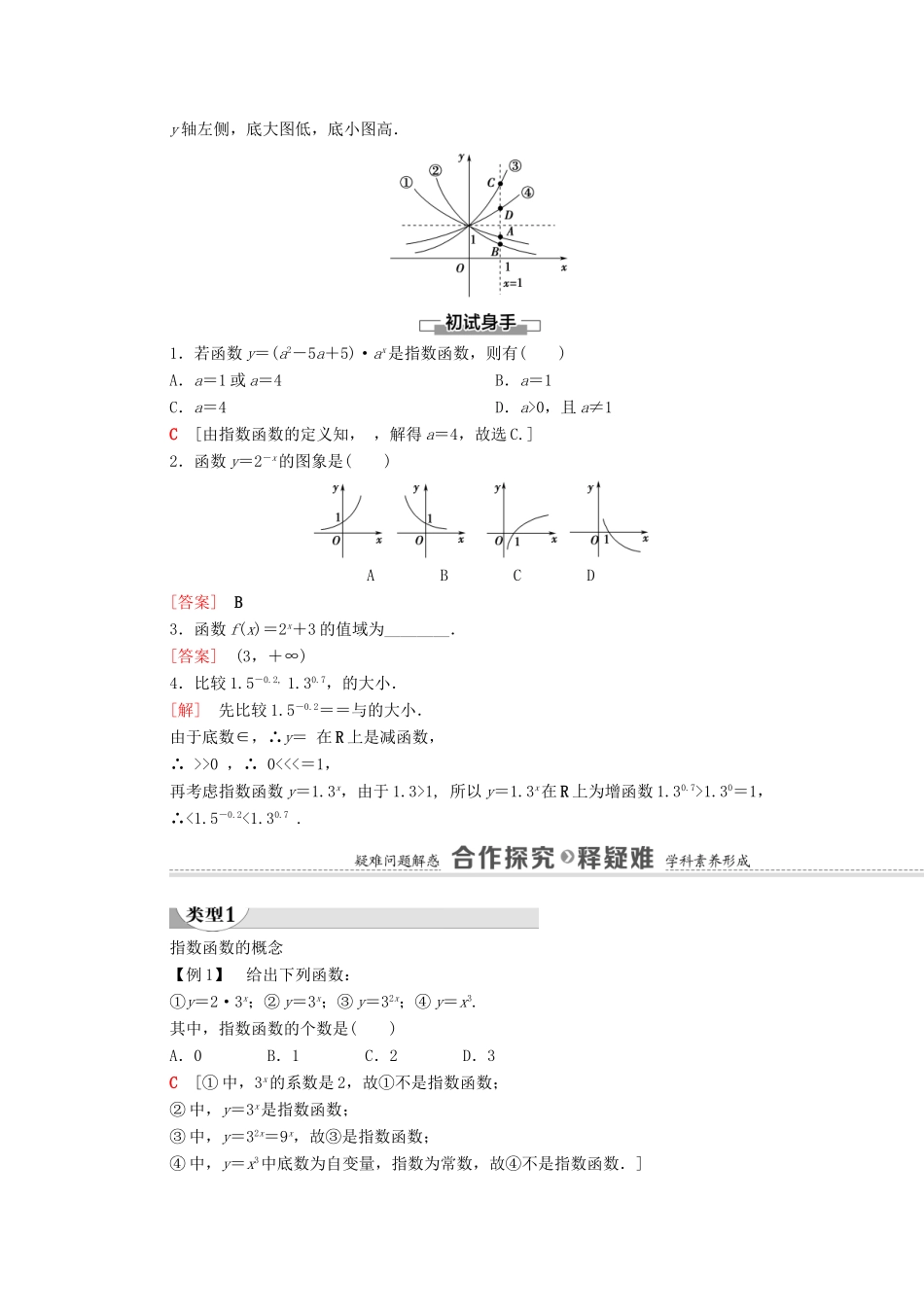
0 时,y > 1 ;当 x<0 时,0 < y < 1 当 x>0 时,0 < y < 1 ;当 x<0 时,y > 1 在上是增函数在上是减函数思考 2:如图是指数函数:(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx 的图象,底数a,b,c,d 与 1 之间的大小关系如何?你能得到什么规律?提示: c>d>1>a>b.规律:y 轴右侧,底大图高,底小图低;y 轴左侧,底大图低,底小图高.1.若函数 y=(a2-5a+5)·ax是指数函数,则有( )A.a=1 或 a=4 B.a=1C.a=4 D.a>0,且 a≠1C [由指数函数的定义知, ,解得 a=4,故选 C.]2.函数 y=2-x的图象是( )A B C D[答案] B3.函数 f(x)=2x+3 的值域为________.[答案] (3,+∞)4.比较 1.5-0.2, 1.30.7,的大小.[解] 先比较 1.5-0.2==与的大小.由于底数∈,∴y= 在 R 上是减函数,∴ >>0 ,∴ 0<<<=1,再考虑指数函数 y=1.3x,由于 1.3>1, 所以 y=1.3x在 R 上为增函数 1.30.7>1.30=1,∴<1.5-0.2<1.30.7 .指数函数的概念【例 1】 给出下列函数:①y=2·3x;② y=3x;③ y=32x;④ y=x3.其中,指数函数的个数是( )A.0 B.1 C.2 D.3C [① 中,3x的系数是 2,故①不是指数函数;② 中,y=3x是指数函数;③ 中,y=32x=9x,故③是指数函数;④ 中,y=x3中底数为自变量,指数为常数,故④不是指数函数.]判断一个函数是指数函数,需判断其解析式是否可化为 y=ax(a>0,且 a≠1)的形式.1.函数 y=(a-2)2ax是指数函数,则( )A.a=1 或 a=3 B.a=1C.a=3 D.a>0 且 a≠1C [由指数函数定义知,所以解得...