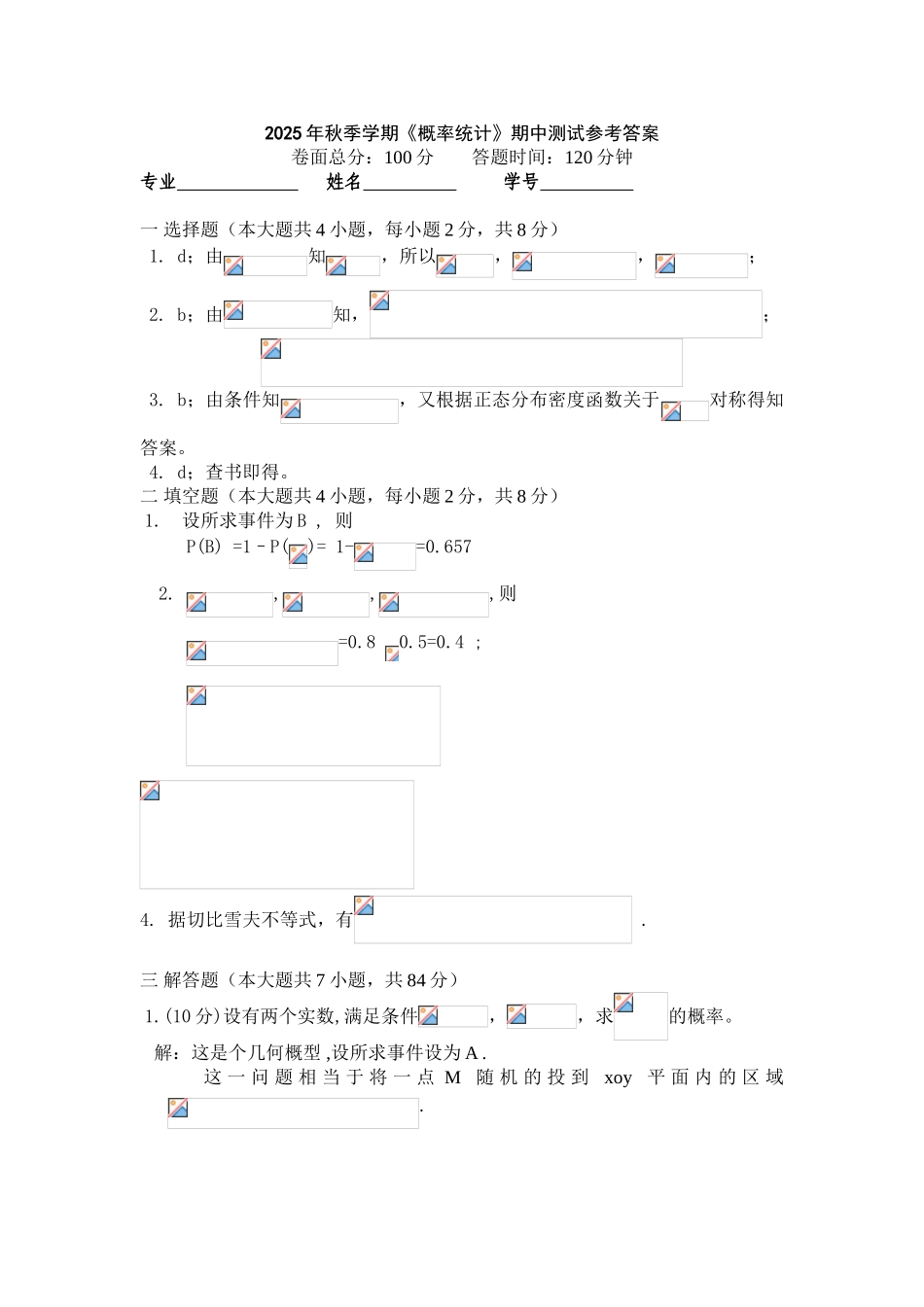
2025 年秋季学期《概率统计》期中试卷 卷面总分:100 分 答题时间:120 分钟专业 姓名 学号 题号一二三四五总分得分一 选择题(本大题共 4 小题,每小题 2 分,共 8 分)1.对于任意两事件与,若,则( ) 2.设随机变量,则( ) 3.设和相互独立,且,,则有( ) 4.下列关于数字特征的运算律,正确的是( ) 二 填空题(本大题共 4 小题,每小题 2 分,共 8 分) 1.设在一次试验中,事件出现的概率为,则在三次独立试验中,事件至少出现 1 次的概率为 ; 2.已知,,,则= ; 3.设随机变量服从参数为 1 的泊松分布,则= ; 4.设随机变量的方差为 2,则根据切比雪夫不等式,有 ;三 解答题(本大题共 7 小题,共 84 分) 1.(10 分)设有两个实数,满足条件,,求的概率。 2.(12 分)已知甲袋中装有 6 只红球,4 只白球;乙袋中装有 8 只红球,7 只白球,丙袋中装有 10 只红球,20 只白球,求:(1)随机地取一只袋,再从该袋中随机地取一只球,该球是红球的概率;(2)已知取到的是红球,求该球是从乙袋中取出的概率。 3.(12 分)设随机变量,现对进行三次独立观测,试求至少有两次观测值大于 3 的概率。 4.(12 分)设随机变量的密度函数为,,试求:⑴ 系数的值; ⑵的分布函数; ⑶概率。5. (14 分)设二维随机变量的联合分布律为Y X-1 0 1120.2 0.1 0.10.1 0.3 0.2 试求:⑴ 关于和的边缘分布律,并推断和是否独立;⑵,及的分布律;⑶,,,,;⑷,,,。6.(14 分)设二维随机变量的联合密度函数为 试求:⑴关于和的边缘密度函数;⑵ 推断和是否独立;⑶的概率密度;⑷ 概率。7.(10 分)一生产线生产的产品成箱包装,每箱的重量是随机的。假设每箱平均重量 50 千克,标准差为 5 千克。若用最大载重量为 5 吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少箱,才能保证不超载的概率大于0.977。(,其中是标准正态分布函数)2025 年秋季学期《概率统计》期中测试参考答案卷面总分:100 分 答题时间:120 分钟专业 姓名 学号 一 选择题(本大题共 4 小题,每小题 2 分,共 8 分)1. d;由知,所以,,;2. b;由知,;3. b;由条件知,又根据正态分布密度函数关于对称得知答案。4. d;查书即得。 二 填空题(本大题共 4 小题,每小题 2 分,共 8 分) 1. 设所求事件为 B , 则 P(B) =1–P()= 1-=0.657 2. ,,,则 =0.8 0.5=0.4 ;...